三个等速旋转点的外心

hbghlyj

圆A与圆B相切于O,点C在圆A上运动,点D在圆B上运动,使得AC,BD的夹角为定值α,求证:OCD的外心E的轨迹为过A,B的圆

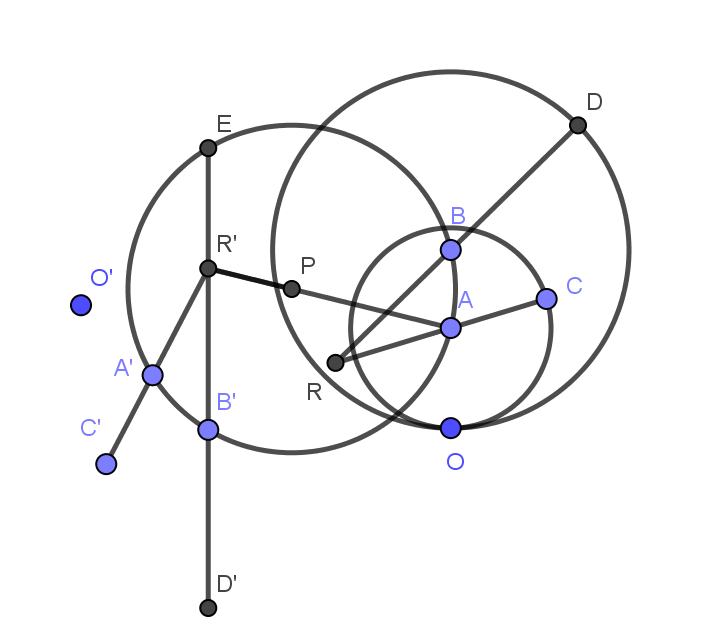
证明：设AC,BD交于R,取P使PA=PB,∠APB=α.T为以P为中心,180°-∠APR的旋转,T(A,B,C,D,O,R)=(A',B',C',D',O',R'),则AR'平分∠A'R'B',设B'R'再次交圆P于E,则T(E)=A,下面证明A为△C'D'O'的外心,从而E为△CDO的外心,易见E的轨迹为圆P.
设β=∠B'R'P,∵C'A'+A'B'=B'D',∴C'A'·B'P+AP·A'B'=B'D'·A'P,C'A'sinβ+APsinα=B'D'sinβ①
∵ABPR共圆,∴A'B'PR'共圆,∴A'R'sinβ+PR'sinα=R'B'sinβ②
①+②,C'R'sinβ+AR'sinα=R'D'sinβ,∴AR'C'D'共圆,又AR'平分∠A'R'B',∴AC'=AD'.
∵∠C'O'D'=∠COD=∠COA-∠BOD=α/2=∠C'R'D'/2=∠C'AD'/2,∴AO'=AC'=AD'.

hbghlyj

可能有关的定理：

P为$\triangle DEF$的密克点，O为$\triangle ABC$的外心，O'为$\triangle O_1O_2O_3$的外心，则PO'=OO'

hbghlyj

两道题的统一：

点A,B,C分别以$O_1,O_2,O_3$为中心等角速度旋转，则△ABC的外心的轨迹loc何时是圆？
现在已经探明的情况：
(1)当三圆共点，以所共之点为A,B,C的起点时，loc是圆(2#)
(2)当三圆两两相切，且AO1∥BO2∥CO3时loc是圆
特别地,当三圆两两相切且圆心共线,一个切点为P,ABCP为矩形时loc是圆；当两圆相切，第三个圆缩到切点时loc是圆(1#)

hbghlyj

用下面的方法可将问题化归到两圆一点的情形，从而将3#(2)化归到1#：
设A,B绕$O_1,O_2$作角速度为$\omega$的圆周运动，$A=O_1+r_1e^{i(\omega t+\phi_1)}，B=O_2+r_2e^{i(\omega t+\phi_2)}$，则$B-A=O_2-O_1+(r_1e^{i\phi_1}+r_2e^{i\phi_2})e^{i\omega t}$，所以B-A绕$O_2-O_1$作角速度也为$\omega$的圆周运动(这里用的是复数法，也可用参数方程+辅助角公式)

hbghlyj

我想我已经把握了这个问题的核心了。就是三个圆有两个位似旋转中心P，也就是使得$PA:PB:PC=r_1:r_2:r_3$的点。让AD,BE,CF从AP,BP,CP开始等速旋转，则O的轨迹是圆。这两个圆的中心都是△ABC的外心O。

位似旋转.ggb (20.19 KB, Downloads: 4469)

2020-5-8 17:25 Upload

Click on the file to download the attachment