平面向量最值

hbghlyj

平面向量$\vec a,\vec b$满足$|\vec a|=4,|\vec b|=3+\sqrt3,\vec a\cdot\vec b=0,f(x)=\langle\vec b+x\vec a,\vec b+(x-1)\vec a\rangle$,则f(x+1)+f(x-1)的最大值为

kuing

a 的模是多少？向量夹角符号用 \langle ... \rangle ，不要直接写 < ... > ，会被认为是小于...大于

facebooker

回复 2# kuing

$|a|=4$
$key:\dfrac{\pi}{3}$

求几何意义的解法

kuing

嗯，有点意思，不是对称取最大

hbghlyj

回复 2# kuing
谢谢指导新手！

kuing

把题目翻译一下先：

如下图，动点 `A`, `B`, `C`, `D` 在直线 `y=b` 上，且 `AB=BC=CD=a`，求 `\angle AOB+\angle COD` 的最大值。

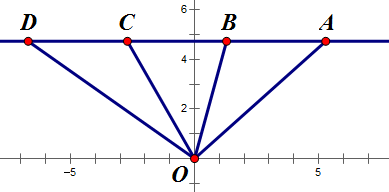
下面先玩玩速度，假设四点以速度 `v` 往右移动，设点 `A` 对原点 `O` 的角速度为 `\omega_A`，则
\[\omega_A=\frac{v\sin A}{OA}=\frac{vb}{OA^2},\]其余点同理，因此
\[
\frac{\rmd(\angle AOB+\angle COD)}{\rmd t}
=vb\left( \frac1{OA^2}-\frac1{OB^2}+\frac1{OC^2}-\frac1{OD^2} \right),
\]也就是说当 `\angle AOB+\angle COD` 取极值时必有 `1/OA^2+1/OC^2=1/OB^2+1/OD^2`，结论虽然好看，但接下来似乎还是免不了要计算？

若记 `BC` 中点的横坐标为 `s`，等式就化为
\[\frac1{(s+1.5a)^2+b^2}+\frac1{(s-0.5a)^2+b^2}=\frac1{(s+0.5a)^2+b^2}+\frac1{(s-1.5a)^2+b^2},\]解得 `s=0` 或
\[16s^4+(24a^2+32b^2)s^2-39a^4-24a^2b^2+16b^4=0,\]所以：
当 `-39a^4-24a^2b^2+16b^4\geqslant0` 时，就只有 `s=0` 一解，即对称时取最大值；
当 `-39a^4-24a^2b^2+16b^4<0` 时，那么取最大值时是
\[s^2=-\frac{3a^2}4-b^2+a\sqrt{3a^2+3b^2}.\]
楼主的题 `a=4`, `b=3+\sqrt3`，属于后者，代入化简得 `s=\pm\sqrt{12-2 \sqrt3}`，但要计算那个角度还是很麻烦？看来得换个法子……

kuing

回复  kuing

$|a|=4$
$key:\dfrac{\pi}{3}$

求几何意义的解法
facebooker 发表于 2020-5-16 15:51

码一下你的解法呗

facebooker

回复 7# kuing
我是设点坐标 算正切。。。 求导 太麻烦了 所以才想知道是不是有简答的解法。