一道导角题

hbghlyj

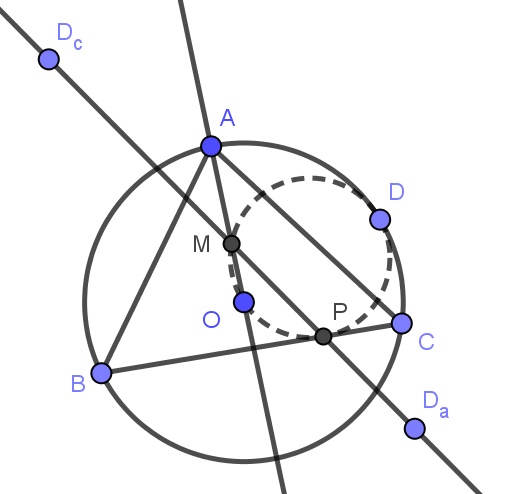
D关于AB,BC的对称点为$D_c,D_a$,直线$D_cD_a$交AO,BC于M,P，求证：ABCD共圆$\Leftrightarrow$DMOP共圆
∵BD=BDc=BDa
∴∠[PM,AB] = ∠[DDa,DB]
∴∠[DDc,DB]=∠[DDc,DDa] + ∠[DDa,DB]= ∠[BA,BP]+∠[PDc,AB]=∠[PDc,PB]
∴BDDcP共圆

∵∠[OM,ADc] =∠[OM,AB] +∠[AB,ADc]=∠[BA,BO]+∠[AD,AB] = ∠[AD,BO]
∠[BD,ADc] =∠[DB,DDc] +∠[DcD,DcA] =∠[DcD,DcB]+∠[DA,DDc]= ∠[AD,BDc]
∴∠[OM,BD] =∠[BDc,BO]
∴∠[OM,BDc]=∠[BD,BO]= ∠[DO,DB]
∴∠[OM,OD] = ∠[BDc,BD]

∵∠[PM,BC] =∠[PM,AB] -∠[BC,BA]=∠[DDa,DB]-∠[DDa,DDc]= ∠[DDc,BD]
∴∠[PM,DDc]=∠[BC,BD]
∴∠[PM,PD] =∠[PM,DDc]+∠[DDc,PD]=∠[BC,BD]+∠[BDc,BC]= ∠[BDc,BD]=∠[OM,OD]
∴MOPD共圆

hbghlyj

D是△ABC外接圆O上一点，AH,CH再交圆O于E,F，DE,DF交BC,AB于P,Q，CO,AO交PQ于M,N，求证$\frac{MD}{ND}\frac{QD}{PD}=\frac{MO}{NO}\frac{QO}{PO}$
证明:由1#得MOQD,NOPD共圆,其半径记为$r_1,r_2$,用正弦定理,
$\frac{MD}{PD}=\frac{QD}{ND}=\frac{MO}{PO}=\frac{QO}{NO}=\frac{r_1}{r_2}$