最大最小值问题

wayne

将函数$|cosx + a| + |sin(2x) + b|$在$x\in\left[0,\frac{\pi}{2}\right]$的最大值记为$M(a,b)$，求$M(a,b)$的最小值（$a,b$是任意实数）。

facebooker

回复 1# wayne


我用曼哈顿距离算的结果是大概0.88  因为有根号 四舍五入了 太丑陋了这个数字  建议把题目改一改吧 算死个人了

kuing

有点坑啊，算了一下，出现了双重根号……
先明天再写……

敬畏数学

回复 2# facebooker
what"s it?

色k

回复 4# 敬畏数学

forum.php?mod=redirect&goto=findpost& … =15320&ptid=2544

kuing

设 `\theta` 为锐角且满足
\[\sin\theta=\frac{-1+\sqrt{33}}8\approx0.593,\]则可计算出
\[\cos\theta=\frac14\sqrt{\frac{15+\sqrt{33}}2}\approx0.805,\]设 $f(x)=\abs{\cos x+a}+\abs{\sin(2x)+b}$，则依题意有
\begin{align*}
2M(a,b)&\geqslant f\left( \frac\pi2 \right)+f(\theta)\\
&=\abs a+\abs b+\abs{\cos\theta+a}+\abs{\sin(2\theta)+b}\\
&\geqslant\cos\theta+\sin(2\theta),
\end{align*}所以
\[M(a,b)\geqslant\frac{\cos\theta+\sin(2\theta)}2,\]经计算可知上式右边的值为
\[\frac1{16}\sqrt{\frac{207+33\sqrt{33}}2}\approx0.880,\]接下来需要说明等号能够取到，事实上，取等的 `(a,b)` 有无穷对，其中一对是
\[(a,b)=\left( -\frac12,\frac12-\frac{\cos\theta+\sin(2\theta)}2 \right),\]也就是要证明
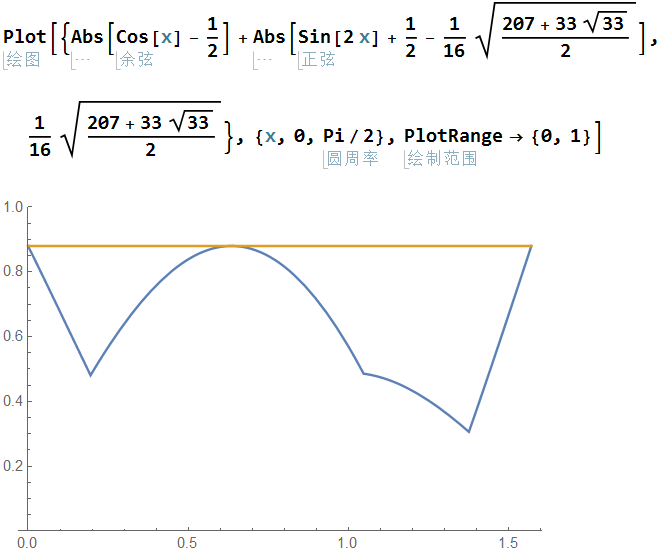
\[\max_{x\in[0,\pi/2]}\left\{ \left| \cos x-\frac12 \right|+\left| \sin(2x)+\frac12-\frac{\cos\theta+\sin(2\theta)}2 \right| \right\}=\frac{\cos\theta+\sin(2\theta)}2,\]可是要证明它似乎挺麻烦，所以暂时耍赖一下——用软件作图代替着先，有机会再补充严格的证明

wayne

回复 2# facebooker
挺好的, 我算的也是这个答案. :)

wayne

回复 6# kuing
我跟2#一样,用的是曼哈顿距离,作图法则.你这纯粹分析,功力深厚!

facebooker

回复 7# wayne


    通常推荐的解法是绝对值恒等式的方法+切比雪夫

wayne

嗯嗯,学习了,谢谢大家. 原题简单些:bbs.emath.ac.cn/thread-17308-1-1.html
我稍微改了下.就是求个验证

kuing

回复 8# wayne

我在开始思考时其实也是根据图形，也是根据图形知道有无穷多对 (a,b) 使之取等，在算出相切的那个 `\theta` 之后，改写成 6# 那个所谓的过程只是装装逼而已……

kuing

补个动图——取等s ：

（第一次手工写 SVG 代码，一般浏览器应该都能看到那正方形会动吧……

wayne

漂亮!会折腾.asymptote 也挺不错的,玩数学的值得推荐.
asymptote.sourceforge.io/