SOP2——两垂心，证垂直

业余的业余

$\triangle ABC$ 中，高 $BE,CF$ 交于点 $H$, $M$ 为 $BC$ 中点，射线 $MH$ 交 $EF$ 于 $K$, 设 $\triangle KBC$ 的垂心为 $L$. 证明：$LH\perp EF.$

乌贼

等价于$ \triangle ABC $外接圆为$ O $，$ AH $交圆于$ G $，$ MH $交圆于$ P $，$ G $为$ BC $与$ DP $交点，$ GK $交OP于$ L $。求证:$ L $为$ KBC $的垂心

乌贼

第一步：先证$ NMH $三点共线（略）
     如图：圆$ O $为$ \triangle ABC $外接圆，$ AN $为直径
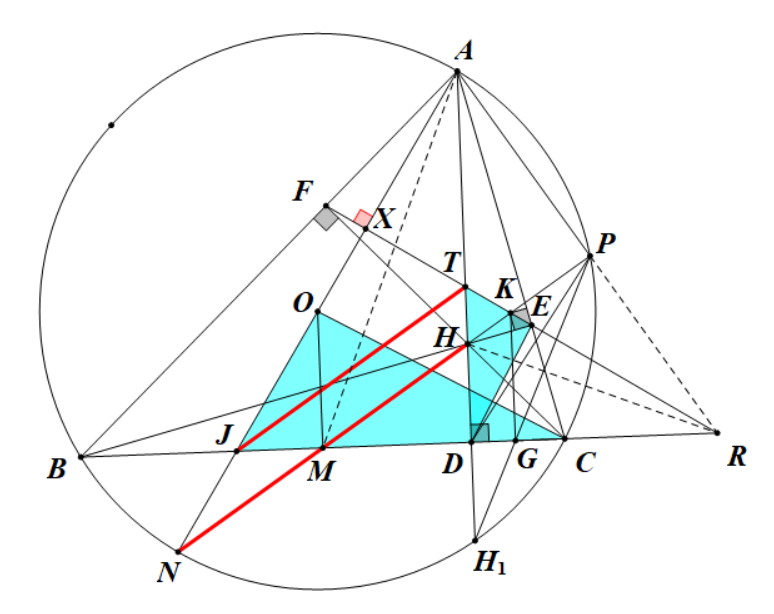
第二步：证明$ KG\perp BC $，或者说证明$ AP、FE、BC $三线共点
    接上图，$ AN $交$ BC $于$ J $，$ AD $交$ EF $于$ T $，$ AN $交$ EF $于$ X $，$ NH $交圆于$ P $，$ AD $交圆于$ H_1 $，$ BC $交$ H_1P $于$ G $，$ FE $交$ BC $于$ R $。
    $ JDTX $四点共圆，有\[ \angle ETD=\angle OJD \]又\[ \angle JOC=2\angle OAC=\angle TED \]所以\[ \triangle TED\sim \triangle JOC\riff\dfrac{ET}{ED}=\dfrac{OJ}{OC}=\dfrac{OJ}{OA}=\dfrac{JM}{MD} \]
   在$ \triangle ETD $中，由角平分线定理知\[ \dfrac{TH}{HD}=\dfrac{ET}{ED} \]故\[ \dfrac{TH}{HD}=\dfrac{JM}{MD}\riff\dfrac{TD}{HD}=\dfrac{JD}{MD}=\dfrac{DR}{DA}\riff\triangle DRH\sim \angle DAM\riff\angle DRH=\angle DAM=\angle  DPH\]即有$ DHPR $四点共圆，也就是$ \angle HPR=90\du  $，$ APR $三点共线
   再由$ \angle KRG=\angle TAX=\angle KPG $知$ KPRG $四点共圆，得\[ \angle KGB=\angle KPR=90\du  \]
第三步:证明$ LHGQP $五点共圆
     另上图（延用上图部分）
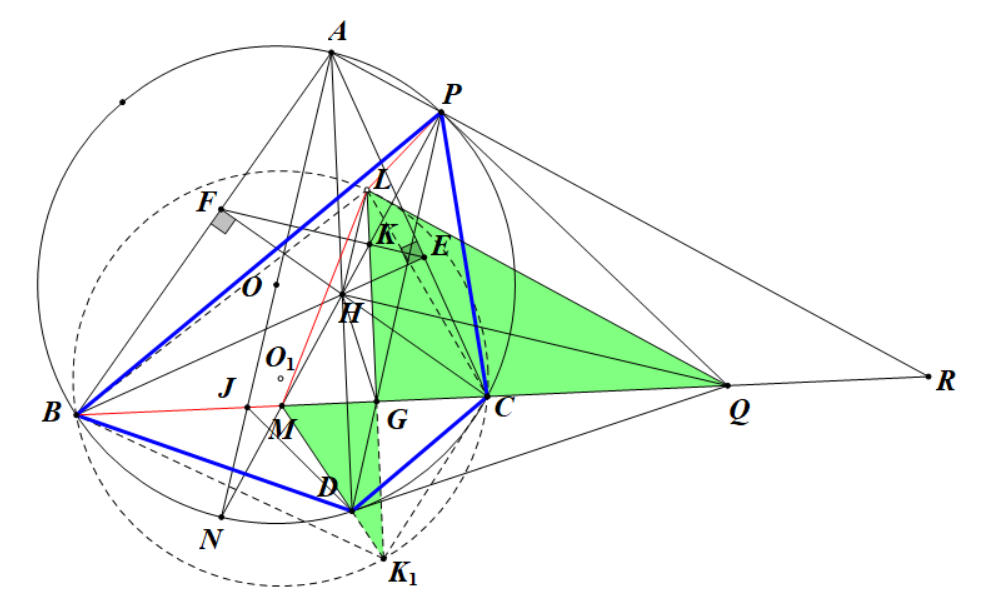
     作$ \triangle AJD $外接圆交$ BR $于$ Q $，由\[ \angle HPG=\angle DAJ=\angle DQJ=\angle HQG \]有$ HPQG $四点共圆，有\[ \angle QPG=\angle QHG=\angle QDG\riff QP=QH=QD \]又\[ \angle CK_1Q=\angle JCK_1-\angle JQK_1=\angle BAD-\angle JAD=\angle BAN=\angle DAC \]知$ QD、DP $均为圆$ O $切线
   作$ \triangle BLC $外接圆$ O_1 $，$ KG $交圆$ O_1 $于$ K_1 $，由对称性知$ MDK_1 $三点共线
   由$ DMPQ、DBPC、BLCK_1 $三个四点共圆有\[ MG\cdot GQ=DG\cdot GP=CG\cdot GB=K_1G\cdot GL\riff\triangle GQL\sim \triangle GK_1M\riff\angle GQL=\angle GK_1M=\angle GKM=\angle GRP\riff LQ\px PR\riff\angle LQP=\angle QPR=\angle PDA=\angle PGL \]即有$ GQPL $四点共圆
   综上有$ HGQPL $五点共圆，有\[ \angle LHP=\angle LGP=\angle PDA=\angle PNA\riff LH\px AN\riff LH\perp EF \]

乌贼

乌贼 发表于 2025-7-13 15:50
第一步：先证$ NMH $三点共线（略）
     如图：圆$ O $为$ \triangle ABC $外接圆，$ AN $为直径
第二步： ...

图中PL、LM、MB又能构成一个直角三角形！