2020年全国卷1理科后三题

lemondian

lemondian

回复 1# lemondian
其中，理20与文21同题，理22与文22同题

lemondian

回复 2# lemondian
(1)20题第2个问题那些解法较为方便？看似答案是（3/2,0)？

（2)22题第2问运算量不小呀

isee

回复 3# lemondian

解几

极点（3/2，0），极线x=6，，


导数

分参+极限，a≥-1/2，未校检
，，，
好题，用e^x展开，显然，不能恒成立。

终于看到一道不是端点的题了，
对分参函数硬求导，求其零点为2，
最后修正为$a\geqslant (7-e^2)/4$。

isee

不等式选讲呢？


===
相当容易，只是x的系数双双不为1，题略。

lemondian

回复 5# isee

isee

这样一看，全国卷1与新高考全国卷1（山东）解析几何都是极经典的题。

facebooker

回复 7# isee

都说是以前考过的某个背景的解析几何 谁能分析一下 这些解几都有啥背景的？

敬畏数学

回复 7# isee
某年某省考过的题，哈哈！
刷题刷爆的同志这次捡便宜了！3分钟搞完这题。哈哈！没有别的会刷题就OK了。有啥今典的？

isee

回复 8# facebooker


此题一般都没有人具体说（其实论坛里已经说了无数次了），要么不愿意说，要么是难以说清晰，我就是属于后者。

但是如果只是仅从结论上说，是这样的（细节不理），直线 $x=m$，椭圆$x^2/a^2+y^2/b^2=1$，则依题中的$CD$过定点$(a^2/m,0)$，其逆命题亦成立。

从解析角度可以参考这个 wenku.baidu.com/view/03534cc283d049649b66588f.html

hbghlyj

极点极线

2.2.2 极点与极线，配极原则

（一）作图原理

定理（配极原则）如果$P$点的极线通过$Q$点，则$Q$点的极线也通过$P$点。

证明：这二阶曲线的方程为$S=0$，$P$点的坐标为$\left(p_{1} p_{2} p_{3}\right)$，$Q$点的坐标为$\left(q_{1}, q_{2}, q_{3}\right)$，于是，$P$点关于$S=0$的极线为$S_{p}=0$，$Q$点关于$S=0$的极线为$S_{q}=0$，因$P$点的极线通过$Q$点，所以有$S_{p q}=0$，但$S_{p q}=S_{q p}$。所以有$S_{q p}=0$，这表示$Q$点的极线$S_{q}=0$通过$P$点。

推论1 两点连线的极点是此二点极线的交点；两直线交点的极线是此二直线极点的连线。

推论2 共线点的极线必共点；共点线的极点必共线。

推论3 设$P A, P B$为二次曲线的切线，若其中$A, B$为切点，则$A B$为$P$点的极线.

定义3.3 如果一个三点形的三个顶点恰是对边的极点，则此三点形叫做自极三点形。

（二）作图举例

例1 、一个完全四点形的四个顶点若在一条二阶曲线上，则这个完全四点形的对边三点形的顶点是其对边的极点。

证明：如下图10，设$X Y Z$是完全四点形$A B C D$的对边三点形，于是$(B G, X E)=-1,(A D, X F)=-1$，所以$E_{1} F$均为关于二阶曲线的共轭点，从而直线$E F$即直线$Y Z$是$X$的极线。

同理，$X Y$是$Z$的极线，由配极原则知，$X Z$是$Y$的极线

例2、已知点$P$不在二阶曲线(c)上，求作$P$点关于(c)的极线。

解：过$P$点作(c)的两条割线，与(c)分别交于$A, B$与$C, D$，如下图所示，设$A C$与$B D$交于点$Q$，$A D$与$B G$交于点$R$，则直线$Q R$就是$P$点的极线。

事实上，由例1可知$P Q R$是自极三点形

hbghlyj

isee 发表于 2020-7-15 09:59
回复 8# facebooker
从解析角度可以参考这个 wenku.baidu.com/view/03534cc283d049649b66588f.html

第15讲:极点与极线的性质

极点与极线是高等几何中的基本且重要的概念,虽然中学数学没有介绍,但以此为背景命制的高考试题经常出现.掌握极点与极线的初步知识,可使我们“登高望远”,抓住问题的本质,确定解题方向,寻找简捷的解题途.

定义:已知曲线G:ax²+bxy+cy²+dx+ey+f=0,则称点P(x₀,y₀)和直线l:ax₀x+b$\frac{y_{0} {x}+x_{0} {y}}{2}$+cy₀y+d$\frac{x+x_{0}}{2}$+e$\frac{y+y_{0}}{2}$+f=0是曲线G的一对极点与极线,点P称为直线l关于曲线G的极点;直线l称为点P关于曲线G的极线.称点P与直线l有“配极关系”,或“对偶关系”,相互为对方的“配极元素”,或“对偶元素”.

特别地,当点P在曲线G上时,点P关于曲线G的极线是曲线G在点P处的切线;圆锥曲线的焦点对应的极线是该焦点对应的准线;圆锥曲线的准线对应的极点是该准线对应的焦点.

[位置关系]:已知点P关于圆锥曲线G的极线是直线l,则三者的位置关系是:①若点P在曲线G上,则直线l是曲线G在点P处的切线;②若点P在曲线G外,则直线l是由点P向曲线G引两条切线的切点弦;③若点P在曲线G内,则直线l是经过点P的曲线G的弦的两端点处的切线交点轨迹.如图:

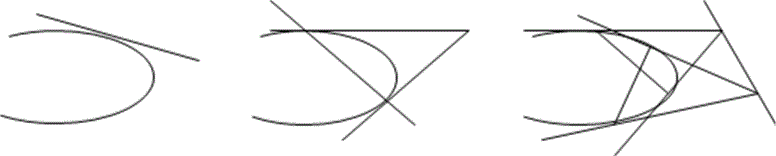
证明:设圆锥曲线G:ax²+bxy+cy²+2dx+2ey+f=0,点P(x_p,y_p),Q(x_Q,y_Q),则点P、Q关于曲线G的极线方程分别为p:ax_px+b$\frac{y_{p} x+x_{m} y}{2}$+cy_py+d$\frac{x+x_{p}}{2}$+e$\frac{y+y_{p}}{2}$+f=0,q:ax_Qx+b$\frac{y_{q} x+x_{q} y}{2}$+cy_Qy+d$\frac{x+x_{Q}}{2}$+e$\frac{y+y_{Q}}{2}$+f=0,则点P的极线通过点Q$\Leftrightarrow$ax_px_Q+b$\frac{y_{p} x_{Q}+x_{p} y_{Q}}{2}$+cy_py_Q+d$\frac{x_{q}+x_{p}}{2}$+e$\frac{y_{q}+y_{p}}{2}$+f=0$\Leftrightarrow$点P(x_p,y_p)在直线q:ax_Qx+b$\frac{y_{q} x+x_{q} y}{2}$+cy_Qy+d$\frac{x+x_{Q}}{2}$+e$\frac{y+y_{Q}}{2}$+f=0上$\Leftrightarrow$点Q的极线也通过点P.

推论1:两点连线的极点是此二点极线的交点,两直线交点的极线是此二直线极点的连线;

证明:设两点A、B连线的极点是P,即点P的极线经过点A、B,由配极原则知点A、B的极线均过点P,即点P是此二点极线的交点;同理可证:两直线交点的极线是此二直线极点的连线.

推论2(共点共线):共线点的极线必共点;共点线的极点必共线.

证明:设点A、B均在直线l上,直线l对应的极点为P,由配极原则知点A、B的极线均过点P,即点A、B的极线必共点;同理可证:共点线的极点必共线.

推论3(中点性质):若圆锥曲线G过点P的弦AB平行于点P的极线,则点P是弦AB的中点.

证明:设P(x₀,y₀),曲线G:ax²+bxy+cy²+2dx+2ey+f=0,则点P的极线方程:ax₀x+b$\frac{y_{0} x+x_{0} y}{2}$+cy₀y+d$\frac{x+x_{0}}{2}$+e$\frac{y+y_{0}}{2}$+f=0,故可设AB:ax₀x+b$\frac{y_{0} x+x_{0} y}{2}$+cy₀y+d$\frac{x+x_{0}}{2}$+e$\frac{y+y_{0}}{2}$+λ=0,由点P(x₀,y₀)在直线AB上$\Rightarrow$ax₀²+bx₀y₀+cy₀²+2dx₀+2ey₀+λ=0$\Rightarrow$λ=-(ax₀²+bx₀y₀+cy₀²+2dx₀+2ey₀)$\Rightarrow$直线AB:ax₀x+b$\frac{y_{0} x+x_{0} y}{2}$+cy₀y+d$\frac{x+x_{0}}{2}$+e$\frac{y+y_{0}}{2}$=ax₀²+bx₀y₀+cy₀²+2dx₀+2ey₀$\Rightarrow$ax₀x+b$\frac{y_{0} x+x_{0} y}{2}$+cy₀y+d$\frac{x+x_{0}}{2}$+e$\frac{y+y_{0}}{2}$+f=ax₀²+bx₀y₀+cy₀²+2dx₀+2ey₀+f,而该直线为以为P中点的中点弦方程,即点P是弦AB的中点.

[比例定理]:若过点P(x₀,y₀)的直线l与曲线G:ax²+bxy+cy²+dx+ey+f=0相交于A、B两点,与直线:ax₀x+b$\frac{y_{0} x+x_{0} y}{2}$+

cy₀y+d$\frac{x+x_{0}}{2}$+e$\frac{y+y_{0}}{2}$+f=0交于点Q,则|PA||QB|=|QA||PB|.

证明:设直线l:$\left\{\begin{array}{l}x=x_{0}+t \cos \theta \\ y=y_{0}+t \sin \theta\end{array}\right.$(t为参数),代入ax₀x+b$\frac{y_{0} x+x_{0} y}{2}$+cy₀y+d$\frac{x+x_{0}}{2}$+e$\frac{y+y_{0}}{2}$+f=0得:(2ax₀cosθ+bx₀sinθ+by₀cosθ+2cy₀sinθ)t+2(ax₀²+bx₀y₀+cy₀²+dx₀+ey₀+f)=0$\Rightarrow$t₀=-2$\frac{a x_{0}^{2}+b x_{0} y_{0}+c y_{0}^{2}+d x_{0}+e y_{0}+f}{2 a x_{0} \cos \theta+b x_{0} \sin \theta+b y_{0} \cos \theta+2 c y_{0} \sin \theta}$;代入ax²+bxy+

cy²+2dx+2ey+f=0得:(acos²θ+bcosθsinθ+csin²θ)t²+(2ax₀cosθ+bx₀sinθ+by₀cosθ+2cy₀sinθ)t+(ax₀²+bx₀y₀+cy₀²+dx₀

+ey₀+f)=0$\Rightarrow$t₁+t₂=-$\frac{2 a x_{0} \cos \theta+b x_{0} \sin \theta+b y_{0} \cos \theta+2 c y_{0} \sin \theta}{a \cos ^{2} \theta+b \sin \theta \cos \theta+c \sin ^{2} \theta}$,t₁t₂=$\frac{a x_{0}^{2}+b x_{0} y_{0}+c y_{0}^{2}+d x_{0}+e y_{0}+f}{a \cos ^{2} \theta+b \sin \theta \cos \theta+c \sin ^{2} \theta}$$\Rightarrow$t₀=$\frac{2 t_{1} t_{2}}{t_{1}+t_{2}}$;而|PA||QB|=

|QA||PB|$\Leftrightarrow$|t₁||t₂-t₀|=|t₁-t₀||t₂|$\Leftrightarrow$t₀=$\frac{2 t_{1} t_{2}}{t_{1}+t_{2}}$成立.

[面积定理]:已知点P关于圆锥曲线G的极线为l,过点P的直线与圆锥曲线G相交于A、B两点,分别过点A、B的两条平行线与直线l交于点D、C,记△APD、△CPD、△BPC的面积分别为S₁,S₂,S₃,则:S₂²=4S₁S₂.

证明:以椭圆G:$\frac{x^{2}}{a^{2}}$+$\frac{y^{2}}{b^{2}}$=1(a>b>0)为例,设P(x₀,y₀),则极线l:$\frac{x_{0} x}{a^{2}}+\frac{y_{0} y}{b^{2}}=1$.设A(x₁,y₁),B(x₂,y₂),并分别过点A、B作l的垂线,垂足分别为D₁、C₁,则$\frac{\left|A D_{1}\right|}{\left|B C_{1}\right|}$=$\frac{\left|\frac{x_{0} x_{1}}{a^{2}}+\frac{y_{0} y_{1}}{b^{2}}-1\right|}{\left|\frac{x_{0} x_{2}}{a^{2}}+\frac{y_{0} y_{2}}{b^{2}}-1\right|}$=$\frac{\left|b^{2} x_{0} x_{1}+a^{2} y_{0} y_{1}-a^{2} b^{2}\right|}{\left|b^{2} x_{0} x_{2}+a^{2} y_{0} y_{2}-a^{2} b^{2}\right|}$(注意到:a²b²=b²x₁²+a²y₁²,a²b²=b²x₂²+a²y²)

=$\frac{\left|b^{2} x_{0} x_{1}+a^{2} y_{0} y_{1}-b^{2} x_{1}^{2}-a^{2} y_{1}^{2}\right|}{\left|b^{2} x_{0} x_{2}+a^{2} y_{0} y_{2}-b^{2} x_{2}^{2}-a^{2} y_{2}^{2}\right|}$=$\frac{\left|b^{2} x_{1}\left(x_{1}-x_{0}\right)+a^{2} y_{1}\left(y_{1}-y_{0}\right)\right|}{\left|b^{2} x_{2}\left(x_{2}-x_{0}\right)+a^{2} y_{2}\left(y_{2}-y_{0}\right)\right|}$(注意到:$\frac{y_{1}-y_{0}}{x_{1}-x_{0}}$=$\frac{y_{2}-y_{0}}{x_{2}-x_{0}}$=k)=$\frac{\left|x_{1}-x_{0}\right|}{\left|x_{2}-x_{0}\right|}$$\frac{\left|a^{2} k y_{1}+b^{2} x_{1}\right|}{\left|a^{2} k y_{2}+b^{2} x_{2}\right|}$.又因$\frac{|A P|}{|B P|}$=$\frac{\left|x_{1}-x_{0}\right|}{\left|x_{2}-x_{0}\right|}$,以下只需证$\frac{\left|a^{2} k y_{1}+b^{2} x_{1}\right|}{\left|a^{2} k y_{2}+b^{2} x_{2}\right|}$=1,即|a²ky₁+b²x₁|=|a²ky₂+b²x₂|,由$\left\{\begin{array}{l}b^{2} x_{1}^{2}+a^{2} y_{1}^{2}=a^{2} b^{2} \\ b^{2} x_{2}^{2}+a^{2} y_{2}^{2}=a^{2} b^{2}\end{array}\right.$$\Rightarrow$b²(x₁-x₂)(x₁+x₂)+a²(y₁-y₂)(y₁+y₂)=0$\Rightarrow$b²(x₁+x₂)+a²k(y₁+y₂)=0$\Rightarrow$a²ky₁+b²x₁=-(a²ky₂+b²x₂)$\Rightarrow$|a²ky₁+b²x₁|=|a²ky₂+b²x₂|$\Rightarrow$$\frac{|A P|}{|B P|}$=$\frac{\left|A D_{1}\right|}{\left|B C_{1}\right|}$,由△ADD₁∽△BCC₁$\Rightarrow$$\frac{|A D|}{|B C|}$=$\frac{|A P|}{|B P|}$,设AC与BD交于点Q,由AD∥BC$\Rightarrow$$\frac{|A D|}{|B C|}$=$\frac{|A Q|}{|Q C|}$$\Rightarrow$$\frac{|A P|}{|B P|}$=$\frac{|A Q|}{|Q C|}$$\Rightarrow$PQ∥BC∥AD$\Rightarrow$S_△BAC=S_△BDC,两边同减S_△BQC得S_△QAB=S_△QDC,又因S_△PQA=S_△PQD,S_△PQB=S_△PQC$\Rightarrow$S_△PCD=S_△QCD+S_△PQD+S_△PQC=S_△QCD+S_△PQA+S_△PQB=S_△QCD+S_△QAB=2S_△QAB$\Rightarrow$S_△QAD=S_△PAD=S₁,S_△QBC=S_△PBC=S₃,S_△QAB=$\frac{1}{2}$S_△PCD=$\frac{1}{2}$S₂,注意到:$\frac{S_{\triangle Q A D}}{S_{\triangle Q A B}} \cdot \frac{S_{\triangle Q H C}}{S_{\triangle Q A B}}$=$\frac{|Q D|}{|Q B|} \cdot \frac{|Q C|}{|Q A|}$=1$\Rightarrow$$S_{\triangle Q A B}^{2}$=S_△QADS_△QBC$\Rightarrow$S₂²=4S₁S₂.