$S_{PAC}·S_{PBD}<S_{PCD}^2$

hbghlyj

过椭圆外一点P作直线交椭圆于两点A,B,
过P作椭圆的两条切线,切点为$T_1,T_2,$
过A,B作两条平行线交$T_1T_2$于C,D,
这个是否是正确的？
$S_{PAC}·S_{PBD}<S_{PCD}^2$

kuing

用软件画了下发现恒有 $\dfrac{\S{PAC}\cdot\S{PBD}}{\S{PCD}^2}=\dfrac14$ ……

kuing

证明也很简单……



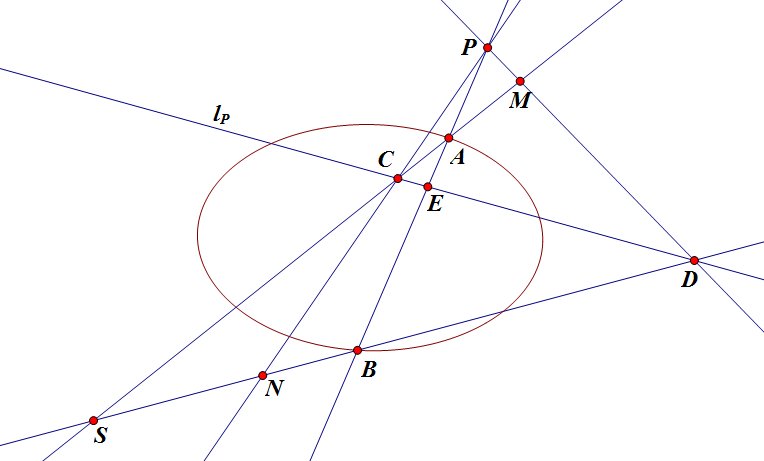
首先如上图，`l_P` 为 `P` 的极线，则 `P`, `A`, `E`, `B` 调和，故 `M`, `A`, `C`, `S` 调和。

而当 `AC` 与 `BD` 平行时，`S` 为无穷远点，则 `A` 为 `CM` 中点，同时 `B` 也为 `DN` 中点。



回到原题，如上图，有
\begin{align*}
\frac{\S{PBD}}{\S{PCD}}&=\frac{BD}{CM}=\frac{BD}{2AC},\\
\frac{\S{PAC}}{\S{PCD}}&=\frac{AC}{DN}=\frac{AC}{2BD},
\end{align*}相乘即得结论。

hbghlyj

回复 3# kuing
对于抛物线、双曲线也一样吗

色k

回复 4# ellipse

是的