求证轨迹是椭圆

hbghlyj

圆A与圆C内切于点B，动圆圆O与圆A外切且与圆C内切，作圆O的一条固定方向的半径OD，求证：D点的轨迹是椭圆
又是很简单的样子....但自己不会证明.......也可能是×的....瑟瑟发抖

kuing

圆 A 与圆 C 内含好像也可以

kuing

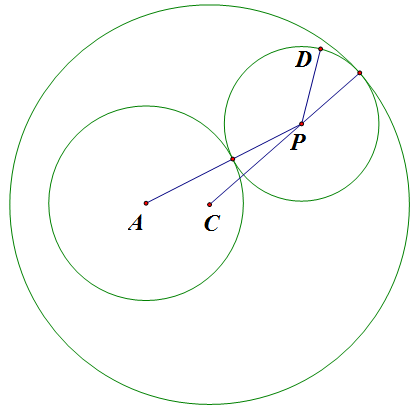
设 `A(-c,0)`, `C(c,0)`, `c>0`，圆 `A` 和圆 `C` 的半径分别为 `r`, `R`, `R-r\geqslant2c`，易知 `PA+PC=R+r`，所以圆心 `P` 的轨迹方程为 `x^2/a^2+y^2/b^2=1`，其中 `a=(R+r)/2`, `b=\sqrt{a^2-c^2}`。

设 `P(a\cos\theta,b\sin\theta)`，由焦半径公式 `CP=a-c\cos\theta`，则圆 `P` 的半径 `r_P=R-CP=R-a+c\cos\theta`，设 $\vv{PD}$ 的固定方向向量为 `(\cos\alpha,\sin\alpha)`，则 `D` 的坐标就是
\[D\bigl( a\cos\theta+(R-a+c\cos\theta)\cos\alpha,b\sin\theta+(R-a+c\cos\theta)\sin\alpha\bigr),\]也就是说 `D` 的轨迹的参数方程为以下形式
\[\led
x&=C_1\cos\theta+C_2,\\
y&=C_3\sin\theta+C_4\cos\theta+C_5,
\endled\]其中 `C_i` 均为常数，由此可见轨迹是二次曲线，而由图形知为闭合曲线，所以要么是圆要么是椭圆。

kuing

其实简单来说就是：
由于动点 `P` 的横纵坐标以及 $\vv{PD}$ 的 `x`, `y` 分量都是 `A\cos\theta+B\sin\theta+C` 的形式，所以 `P`, `D` 的轨迹都是二次曲线，而且不会是抛物线和双曲线。

楼主的命题之所以成立，完全就是因为动圆 `P` 的半径能写成 `A\cos\theta+C` 的形式……