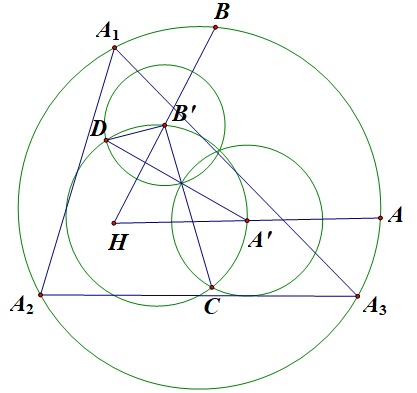
Last edited by hbghlyj 2023-4-26 12:55A,B的西姆松线分别交九点圆于A’,D;B’,C,其中A’,B’为AH,BH中点,则圆A’(A’C)和圆B’(B’D)的一个交点为直线B’C,A’D的交点,另一个交点在九点圆上
证明:因为$\overparen{A'B'}$与$\overparen{AB}$关于$H$位似;两条西摩松线之间的角与这弧所对的圆周角相反,所以
$$∠[A’D,B’C]=\frac{\overparen{BA}}2=\frac{\overparen{B'A'}}2=∠[B'D,A'D]$$故两圆的一个交点为直线B’C,A’D的交点.
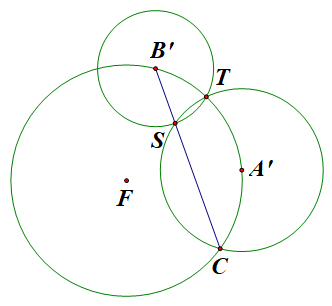
要证明另一个交点在九点圆上,重新表述为:以圆F上的点A',B'过S作圆,B'S与圆F再交于C,C在圆A'上,则圆A',B'的另一个交点T在圆F上
证明:因为S,T关于A'B'对称,所以A'B'平分∠TB'C,又A'T=A'C,所以A'B'CT共圆.
∠[,]表示有向角,\overparen表示有向弧 |