Last edited by hbghlyj 2020-8-1 21:091.AC,AB上的内切圆切点为E,F,旁切圆切点为E',F',I'是I关于EF的对称点,求证$I'H\bot E'F'$

第一个注意到BC中点,AH中点和H在角平分线上的垂足共线。
2.AH交圆O于D, AI交圆O于L,若∠AIH=90°,求证:∠IDL=90°
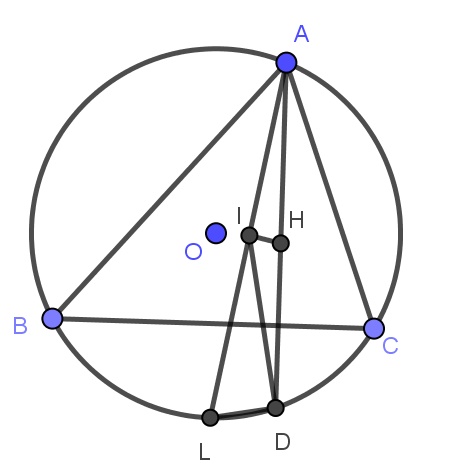
注意到I’是垂心,过I’作E’F’平行线交AB、AC于NM,I’H交EF于T,证明ET/FT=MI’/NI’,得I’T垂直MN即可。
第1,2题来自纯几何吧4501
3.圆O的弦AF⊥PE,EF交BC于S,SD⊥PE于D,求证:△APD,BPD,CPD的垂心共线
注意到EP关于ABC的垂极点是EP关于ABC的simson线的交点即可
来自纯几何吧4499
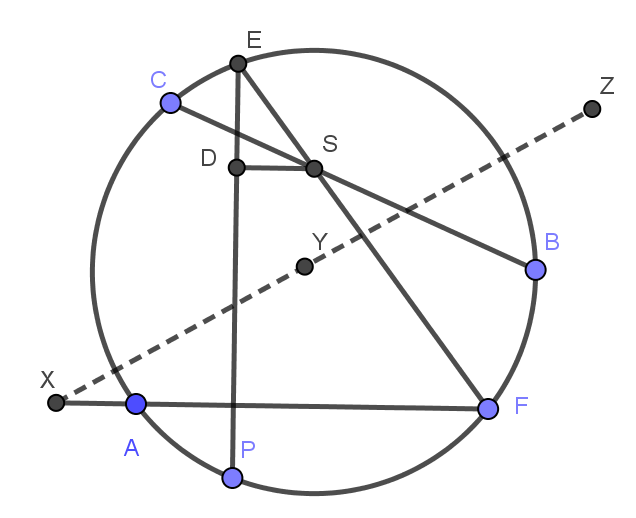
4.在E关于ABC的西姆松线上任取一点D,延长ED交圆于点P,则△APD,BPD,CPD垂心共线且连线垂直于西姆松线

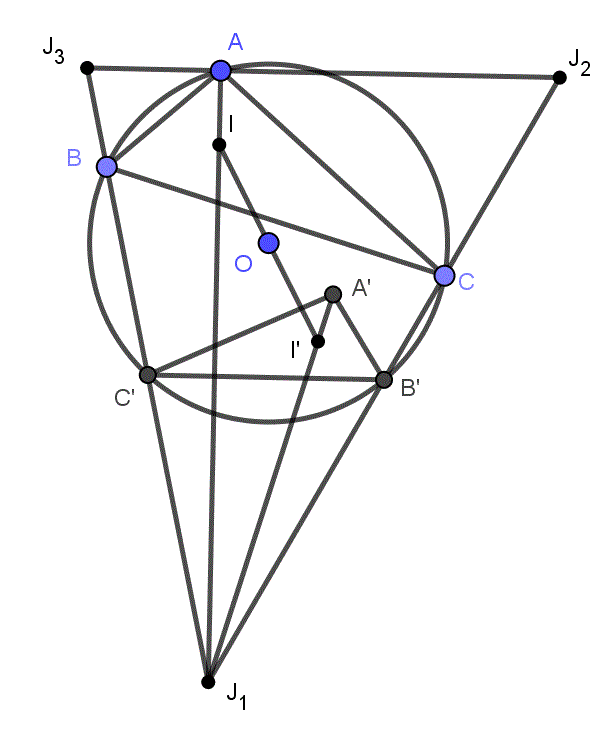
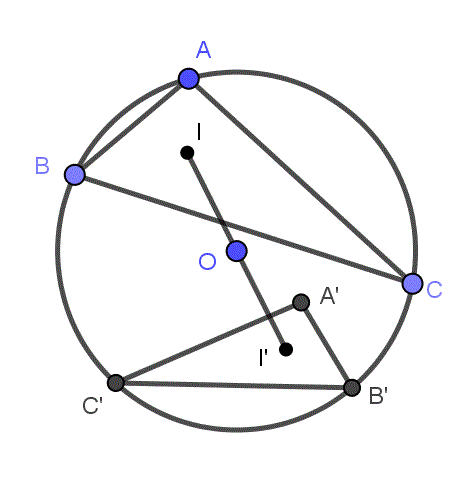
5.△ABC内接于圆O,E,F分别为弧ACB和弧ABC的中点,D,A在EF的同侧,且△DEF~△ABC,I是△ABC的内心,求证OI∥AD
|