|
|
存个档:
v6 23:04:01

这个题怎么撸,头晕
kuing 23:12:20
将 =1 变成 =a^2,条件就变成 (a-b)*(a-c)=0 这样可能好入手点
画图变成一个圆上两点和圆内一点垂直啥的
kuing 23:32:49
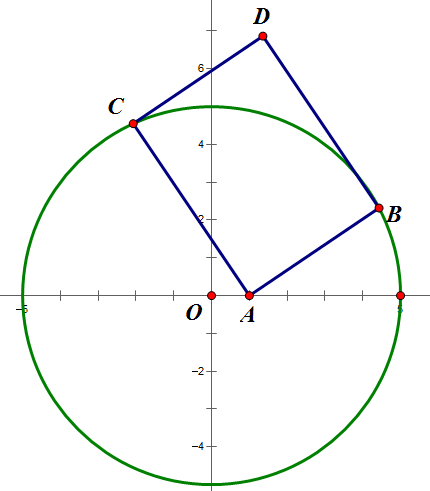
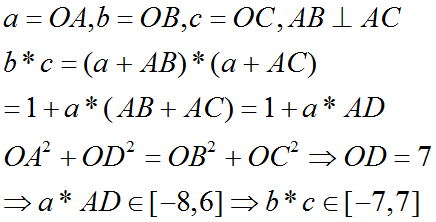
以上字母全是向量,懒得打箭头
事实上,上述解法在空间中也是适用的,就是圆变成球,平方和相等那个性质不限于平面,最后 a*AD 的范围也是,所以在空间也没问题。
当然,最好还是补充一个纯代数解法,其实就是将上述想法改写一下即可:
解:因为 `1=\bm a^2`,所以条件变成 `(\bm a-\bm b)\cdot(\bm a-\bm c)=0`,则
\[\bm a^2+(\bm b+\bm c-\bm a)^2-\bm b^2-\bm c^2=2(\bm a-\bm b)\cdot(\bm a-\bm c)=0,\]得到
\[|\bm b+\bm c-\bm a|=\sqrt{\bm b^2+\bm c^2-\bm a^2}=7,\]所以
\[\bm b\cdot\bm c=\bm a\cdot(\bm b+\bm c-\bm a)\in[-7,7].\] |
Rate
-
View Rating Log
|