Last edited by hbghlyj 2020-8-22 14:45P,Q等角共轭,Q的垂足三角形为DEF,则P的圆塞瓦三角形和Q关于DEF的垂足三角形位似,且P,Q为对应点
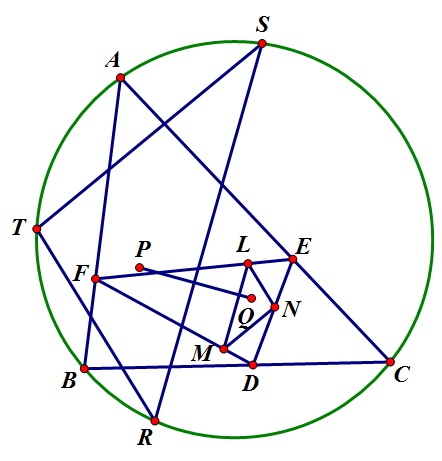
证明:∵∠[MN,BC]=∠[MN,DE]+∠[DE,BC]=∠[MQ,DQ]+∠[DE,BC]=∠[DF,BC]+∠[DE,BC]=∠[QF,QB]+∠[QE,QC]=∠[AB,QB]+∠[AC,QC]=∠[PB,BC]+∠[PC,BC]=∠[SB,BC]+∠[ST,SB]=∠[ST,BC]
∴MN∥ST,同理可得LMN与RST的各边平行,所以位似
∵∠[AB,AP]=∠[AQ,AC]=∠[QF,EF]=∠[AB,QL],
∴AP∥QL,同理可得BP∥QM,所以P,Q位似对应
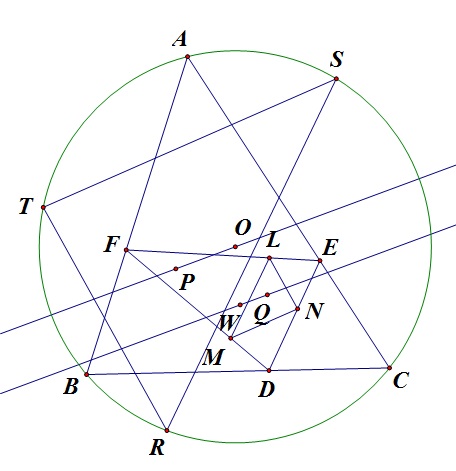
推论:W是Q关于DEF的等角共轭,则PO∥QW
证明:设P关于RST的反垂足三角形中PV等角共轭则圆O为垂足圆,且P,Q;V,W位似对应,所以POV∥QW
|