Last edited by hbghlyj 2020-9-3 22:53几何画板的画多边形工具
多边形的顶点序列:依次选中$v_1,v_2,\cdots,v_n$,然后选任何一个顶点$v_i(1\le i\le n)$,生成多边形$v_1v_2\cdots v_n$,它的边是$v_1v_2,v_2v_3,\cdots,v_nv_1$
简化规则:如果相邻的三个顶点$v_{i-1},v_i,v_{i+1}$共线(不论这三点在直线上的顺序),则可以把$v_i$去掉而不改变多边形的内部.
多边形的内部遵循奇偶规则:平面内的任何一点P,引出一条射线,注意不要经过多边形的顶点,如果射线与多边形的交点的个数为奇数,则点P在多边形的内部,如果交点的个数为偶数,则点P在多边形的外部。
举例:
利用奇偶规则可以画"不连续的多边形"的内部,请看下面这个多边形内部是如何画出来的:
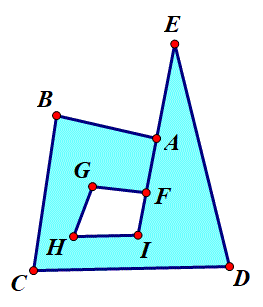
A,B,C,D,E,F,G,H,I
或A,B,C,D,E,I,H,G,F
或E,D,C,B,A,F,G,H,I
或E,D,C,B,A,I,H,G,F
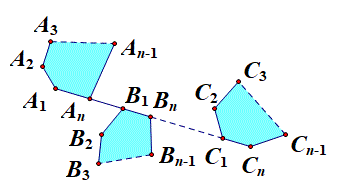
m个n边形,每个多边形取一条边,总共n条边共线,则可以画出它们的并集
$A_1A_2A_3\cdots A_{n-1}A_nB_1B_2B_3B_{n-1}B_n\cdots C_1C_2C_3\cdots C_{n-1}C_n$
由于$A_1,A_n;B_1,B_n;\cdots;C_1,C_n$在直线上是对称的,所以可以把每个多边形的顶点顺序颠倒,总共$2^m$种画法,例如
$A_1A_2A_3\cdots A_{n-1}A_nB_nB_{n-1}\cdots B_3B_2B_1\cdots C_1C_2C_3\cdots C_{n-1}C_n$
|