最少的点，视线覆盖单位球

hbghlyj

有限集$S\subset\mathbf{R}^n$,$E=\{v\in\mathbf{R}^n\mid v\cdot v\ge1\}$,对任意p∈$\mathbf{R}^n$,存在q∈S使得(pq)⊆E,求#S的最小值f(n).
一些思路
当n=1时,E是直线上一个线段的外部,必须有S的两个点在线段两侧,所以至少有两个点了,即f(1)=2.
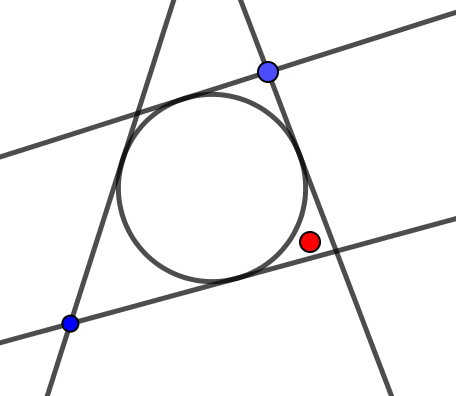
当n=2时,E是平面上单位圆的外部,这时如果S只有两个点(图中蓝点),取q为红点,则这两个点与q的连线都不能完全包含在E内,所以S至少有3个点,这时取单位圆的一个外切三角形的顶点即可.故f(2)=3.

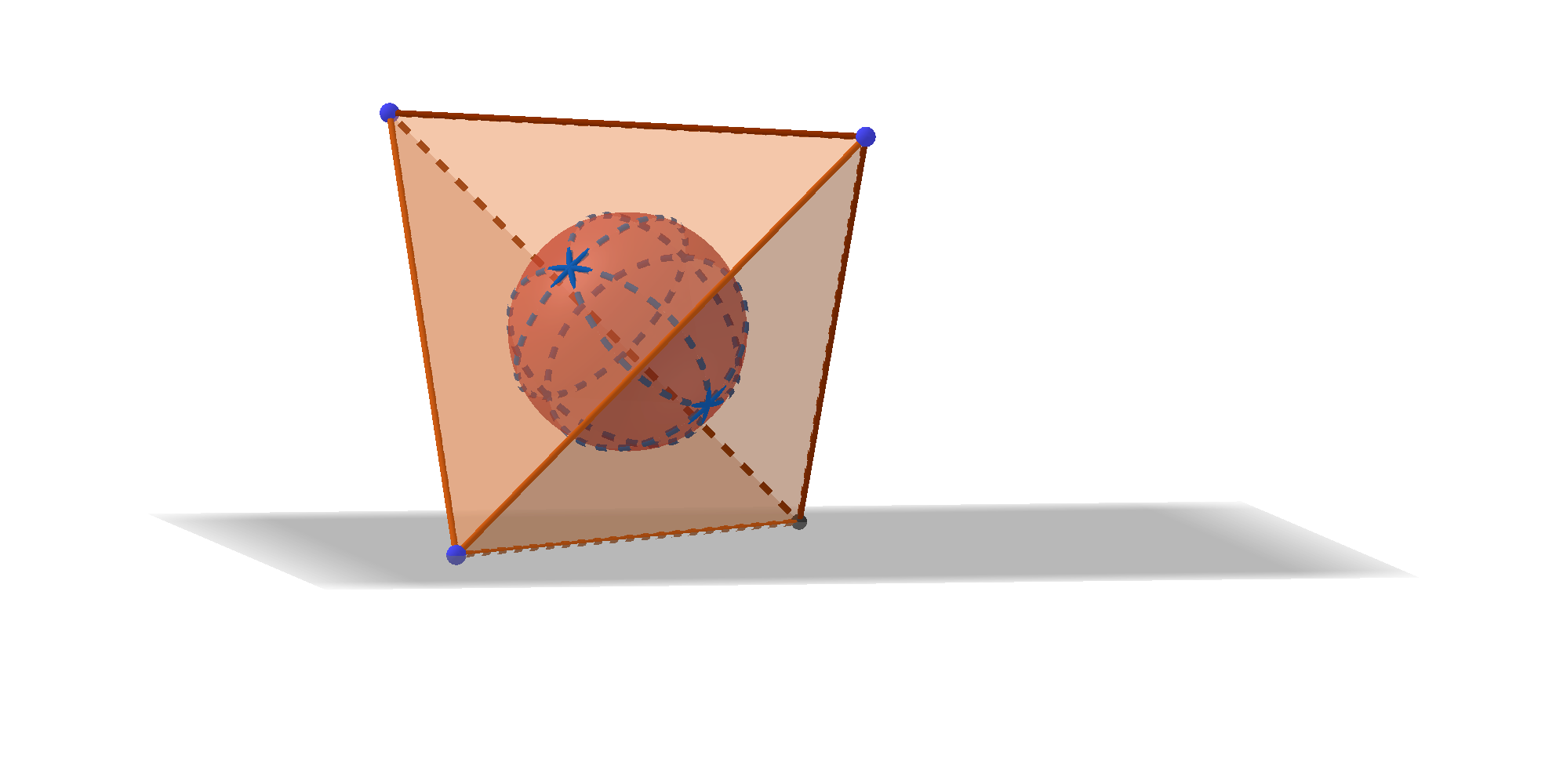
当n=3时,E是空间上单位球的外部,这时如果S只有三个点,容易想象,会留出覆盖不到的点,所以S至少有3个点,这时取单位圆的一个外切三角形的顶点即可.故f(3)=4.比如正四面体的四个顶点.
当n=4时,?????

注：(pq)表示线段pq,#S表示S的元素个数.

青青子衿

回复 1# hbghlyj

有限集$S\subset\mathbf{R}^n$,$E=\{v\in\mathbf{R}^n\mid v\cdot v\ge1\}$,对任意p∈$\mathbf{R}^n$,存在q∈S使得(pq)⊆E,求#S的最小值f(n).
f(2)=2
f(3)=4
注：(pq)表示线段pq,#S表示S的元素个数.
hbghlyj 发表于 2020-9-6 20:50

二维的情形应该是三个点吧？我想到的是单位圆的外切三角形；如果是两个点的话，那就是两个互为对径的无穷远点。

另外，可以参考拓扑学中的“Lusternik–Schnirelmann 定理”
zhihu.com/question/308780503/answer/692447872

hbghlyj

回复 2# 青青子衿
的确f(2)=3。我刚才㗅。已经改正了。谢谢您答疑解惑。