来自人教群：$\sum\frac1{2(a+b+c)^2+9b^2+9c^2}\le\dots$

kuing

河北学生lky 2020/11/7 21:22:28

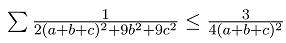
放一个不等式

简直就是为下面这种 CS 方法出的题，系数凑得刚刚好……

右边分母乘过去后易知原不等式等价于
\[\sum\frac{b^2+c^2}{2(a+b+c)^2+9b^2+9c^2}\geqslant\frac16,\]由 CS 有
\begin{align*}
\LHS&\geqslant\frac{\left( \sum\sqrt{b^2+c^2} \right)^2}{6(a+b+c)^2+18(a^2+b^2+c^2)}\\
&=\frac{2(a^2+b^2+c^2)+2\sum\sqrt{a^2+b^2}\sqrt{a^2+c^2}}{6(a+b+c)^2+18(a^2+b^2+c^2)}\\
&\geqslant\frac{2(a^2+b^2+c^2)+2\sum(a^2+bc)}{6(a+b+c)^2+18(a^2+b^2+c^2)}\\
&=\frac16.
\end{align*}