卫星定位基本原理

zhcosin

这只是最基础的原理,有大量的实际问题并未考虑在内,首先就是如何确定各参考点的经纬坐标,其次如何得到测点到各参考点的距离,通过发送电磁信号并测量传播用时的方法,又涉及到一个高科技问题,因为电磁信号传播速度为光速,那么时间精度便是一个难题。此外,限于国土面积限制,如何把参考点都设在国内,那么定位服务将仅限于自己国家范围,如果在海外基地或者测量船上搭建移动基站,那么还涉及到移动参考点问题,诸如此类,这是一个非常复杂的系统工程。

isee

回复 1# zhcosin

哇，书又更新了~

yuzi

zhcosin

加了点点屁话。

hbghlyj

Navigation equations
Hyperboloids
If the pseudorange between the receiver and satellite $i$ and the pseudorange between the receiver and satellite $j$ are subtracted, $p_i-p_j$, the common receiver clock bias (b) cancels out, resulting in a difference of distances $d_i-d_j$.

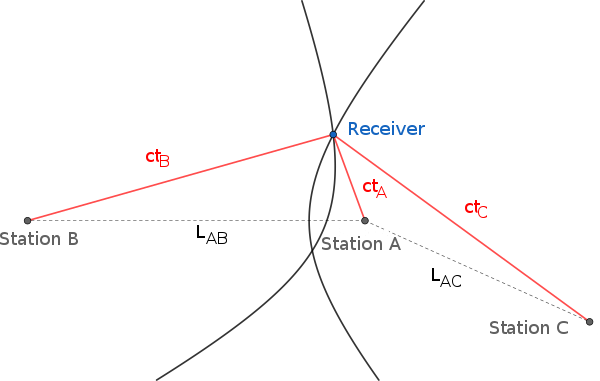
The locus of points having a constant difference in distance to two points (here, two satellites) is a hyperbola on a plane and a hyperboloid of revolution (more specifically, a two-sheeted hyperboloid) in 3D space (see Multilateration). Thus, from four pseudorange measurements, the receiver can be placed at the intersection of the surfaces of three hyperboloids each with foci at a pair of satellites. With additional satellites, the multiple intersections are not necessarily unique, and a best-fitting solution is sought instead.

Inscribed sphere The receiver position can be interpreted as the center of an inscribed sphere (insphere) of radius $bc$, given by the receiver clock bias $b$ (scaled by the speed of light $c$). The insphere location is such that it touches other spheres. The circumscribing spheres are centered at the GPS satellites, whose radii equal the measured pseudoranges $p_i$. This configuration is distinct from the one described above, in which the spheres' radii were the unbiased or geometric ranges $d_i$.