垂心连线证明垂直

hbghlyj

D为$\triangle$ABC内角A的平分线上一点(异于A) ,E,F分别为$\triangle$ACD,$\triangle$ABD的垂心.G为BC中点.证明DG⊥EF.

hbghlyj

题源：纯几何吧2761推广
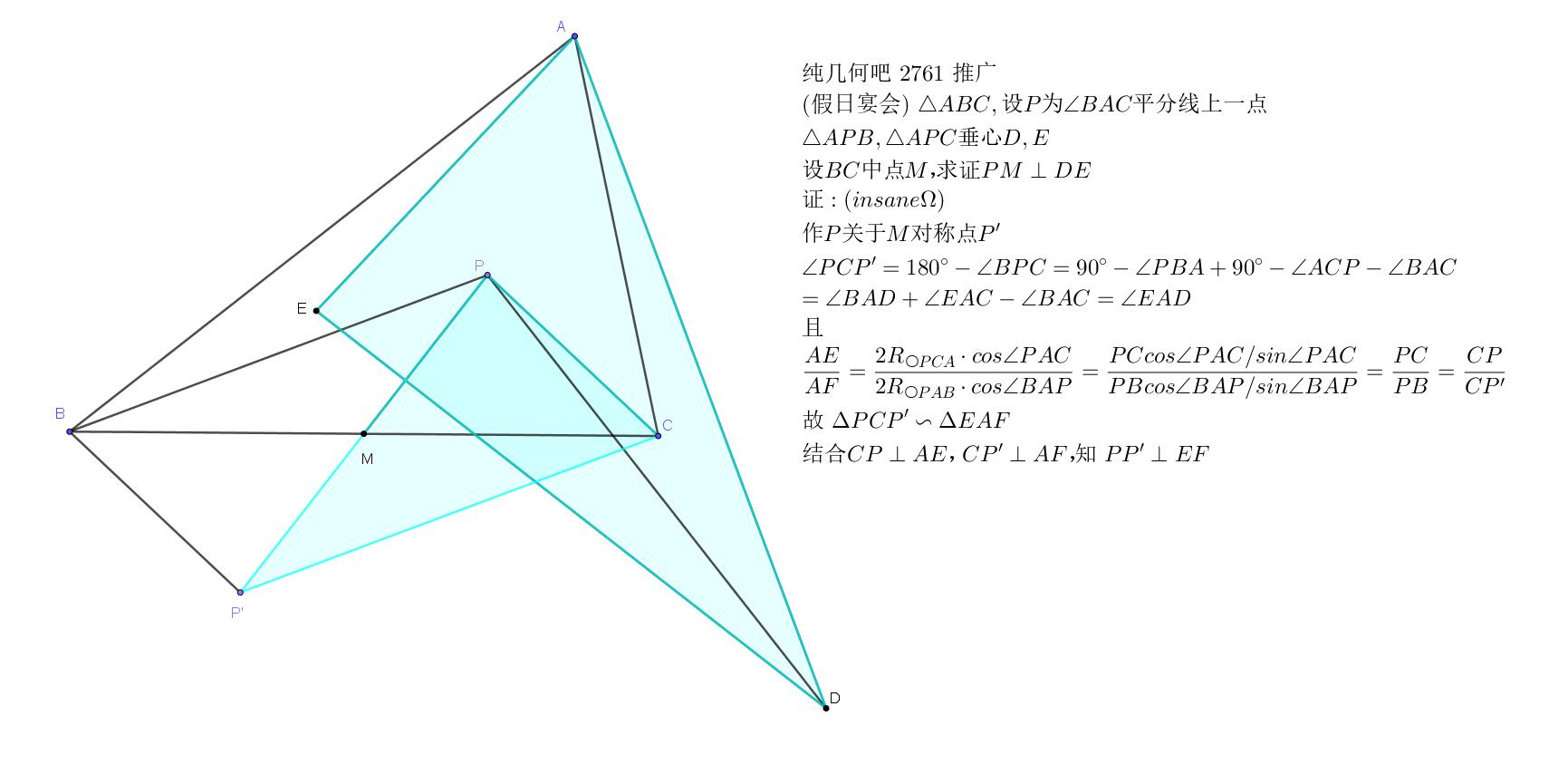
证: (insaneΩ)
方法1:作P关于M对称点P'
∠PCP'= 180°-∠BPC= 90°-∠PBA+ 90°-∠ACP-∠BAC=∠BAD +∠EAC-∠BAC=∠EAD
且${AE\over AF}={2R_{\odot PCA}•\cos∠PAC\over 2R_{\odot PAB}•\cos∠BAP}={PC cos∠PAC/sin∠PAC \over PB cos∠BAP/sin∠BAP}={PC\over PB }={CP\over CP'}$,故△PCP'~△EAF.
结合CP⊥AE,CP'⊥AF,知PP'⊥EF

方法2:

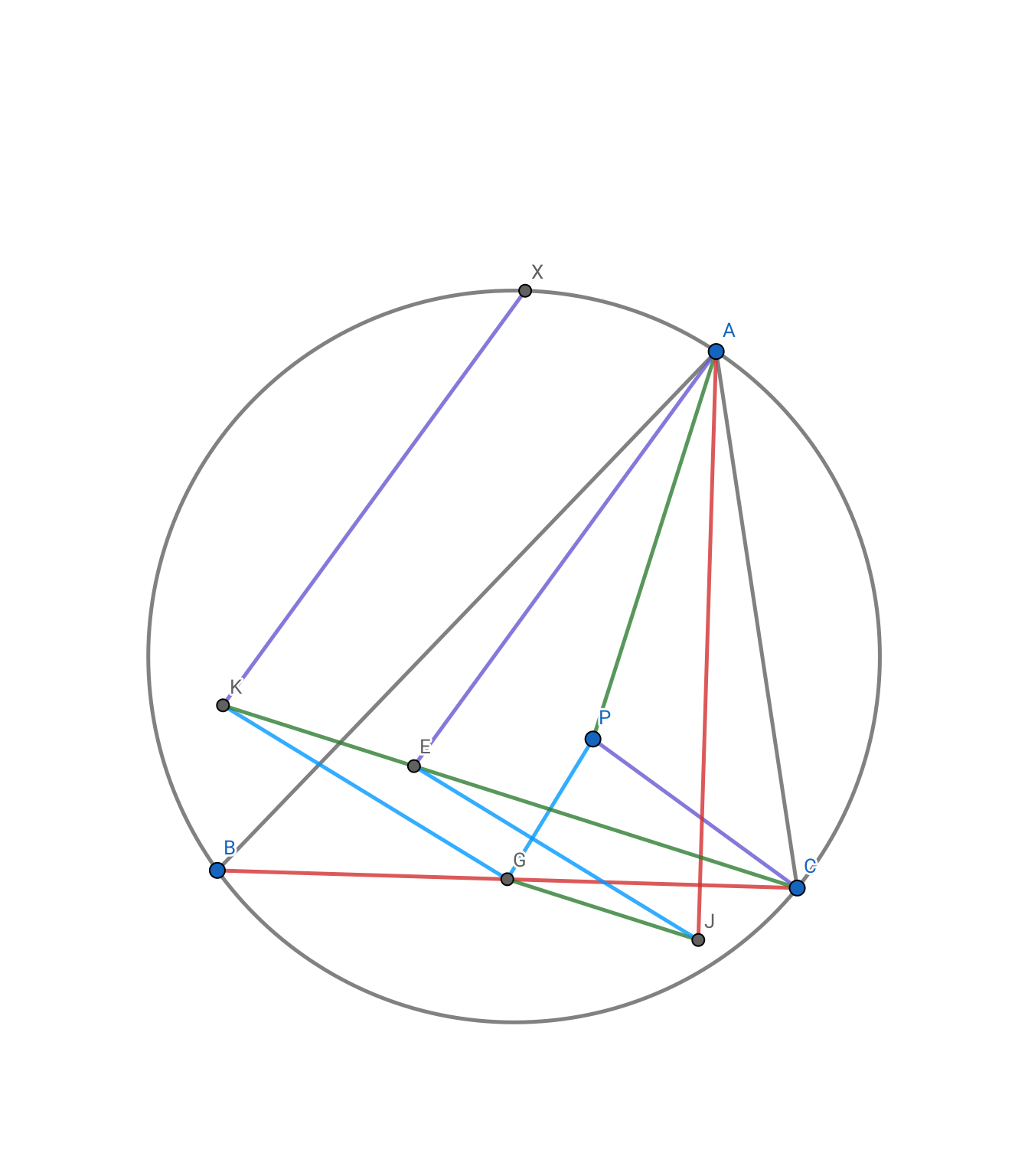
其中X的生成本质是过G的BC垂线与过A的AP垂线的交点.
设U,V,W分别为BC垂线向,PG垂线向,AD垂线向的无穷远点.过G垂直于AP的直线交过A垂直于BC的直线于J,过C的AP垂线交过G的PG垂线于K,对AEW与UVG用笛沙格定理知只需证$AK\bot CP$.这是显然的.

hbghlyj

回复 1# hbghlyj
用重心坐标算
不到1秒

1. ptD = {u, b, c};
2. ptE = Ortocentro[{ptA, ptC, ptD}];
3. ptF = Ortocentro[{ptA, ptB, ptD}];
4. ptG = {0, 1, 1};
5. EF = Recta[ptE, ptF];
6. DG = Recta[ptD, ptG];
7. SonPerpendiculares[EF, DG]

Copy the Code

--------------
下载Mathematica插件baricentricas.nb