对角线夹角60°的梯形 对角线长和下底边长的不等式

hbghlyj

梯形ABCD中AD∥BC,AD<BC,∠AOB=$60^∘$,求证AB+CD≥BC

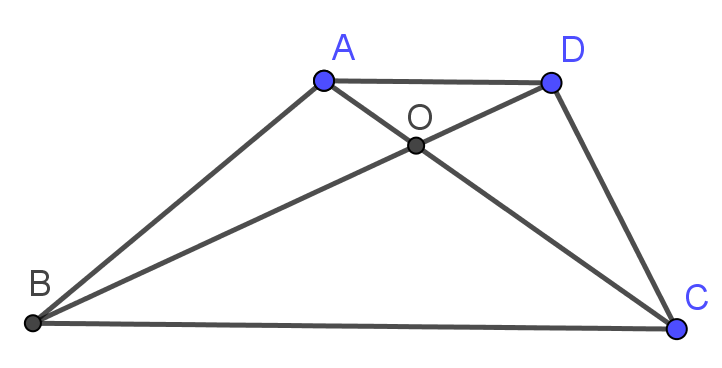
证明:设AC,BD交于O,设$\frac{AD}{BC}=k$(0<k<1),BO=x,CO=y,则AO=ky,DO=kx,在△AOB,△DOC中用余弦定理,只要证$\sqrt{k^2x^2+y^2-kxy}+\sqrt{x^2+k^2y^2-kxy}\geq\sqrt{x^2+y^2+xy}.$
平方得,$-k^2\left(x^2+y^2\right)+\left(2k+1\right)xy\leq2\sqrt{\left(k^2x^2+y^2-kxy\right)\left(x^2+k^2y^2-kxy\right)}\ldots(1)$.
再平方,$(-k^2\left(x^2+y^2\right)+\left(2k+1\right)xy)^2\leq4\left(k^2x^2+y^2-kxy\right)\left(x^2+k^2y^2-kxy\right)\ldots(2)$.[不等式(2)成立可以推出(1)成立,反过来则不能]
等价于证$-(-k^2\left(x^2+y^2\right)+\left(2k+1\right)xy)^2+4\left(k^2x^2+y^2-kxy\right)\left(x^2+k^2y^2-kxy\right)=(2k^4-4k+3)x^2y^2+(4k^2-k^4)(x^4+y^4)+2(k^2-2k)xy(x^2+y^2)\ge0$
注意到$x^4+y^4\ge 2x^2y^2,x^2+y^2\ge 2xy$,
消去$x^2y^2$,只需证$2k^4-4k+3+2(4k^2-k^4)+4(k^2-2k)\ge0$,也就是$(2k-1)^2\ge0$显然成立.
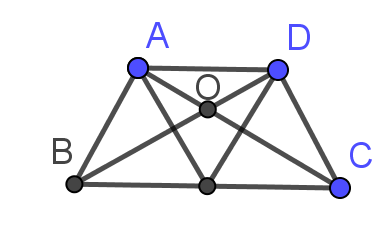
取等时,x=y且$k=\frac12$,这时梯形ABCD是由三个等边三角形拼起来的:

hbghlyj

衍生题:
梯形ABCD,$AD\parallel BC$,当AB+CD=BC时，AC与BD交角最小是多小？

hbghlyj

回复 2# hbghlyj
设$c=\cos AOB$,则AB+CD=BC等价于$\sqrt{k^2x^2+y^2-2kxyc}+\sqrt{x^2+k^2y^2-2kxyc}=\sqrt{x^2+y^2+2xyc}.$
问题转化为:
求$c\in(0,60^\circ]$的最小值,使得存在正数x,y和0<k<1,满足
$4 \left(c^2-1\right) x^2 y^2-4 k^2 \left(c x^3 y+c x y^3+x^4+y^4\right)+8 c k x y \left(2 c x y+x^2+y^2\right)+k^4 \left(x^2-y^2\right)^2=0$

kuing

梯形ABCD中AD∥BC,AD<BC,∠AOB=$60^∘$,求证AB+CD≥BC
hbghlyj 发表于 2020-12-29 23:35

还是撸几何法吧，虽然有讨论……

不妨设 `OB\geqslant OC`，作 `\angle BOC` 的角平分线交 `BC` 于 `E`，作 `A` 关于 `BD` 的对称点 `A'`，作 `D` 关于 `AC` 的对称点 `D'`，由 `\angle BOC=120\du` 知两对称点均在角平分线上。

若 `OB=OC` 则两对称点重合，此时结论显然成立，当 `OB>OC` 时 `OA<OD`，即 `A'` 在 `O` 与 `D'` 之间，然后分类讨论：


当 `A'`, `D'` 都在线段 `OE` 上，如上图，则由 `\angle BEA'` 为钝角有 `BA'>BD'`，故 `AB+CD=BA'+CD'>BD'+CD'\geqslant BC`；


当 `A'`, `D'` 在 `E` 的两则，如上图，则由 `\angle BEA'`, `\angle CED'` 均为钝角有 `BA'>BE` 及 `CD'>CE`，故 `AB+CD=BA'+CD'>BE+CE=BC`；


当 `A'`, `D'` 都不在线段 `OE` 上，如上图，则由 `\angle CED'` 为钝角有 `CD'>CA'`，故 `AB+CD=BA'+CD'>BA'+CA'\geqslant BC`。

综上即得证。

kuing

回复 4# kuing

按这个证明，当 `OB>OC` 时，只要确 `OA<OD` 就可以推出结论而不一定需要梯形？