来自人教群的简单三元不等式

kuing

鄂D山羊无角(7048*****) 2021/1/21 9:33:28
请问：x,y,z>0，则

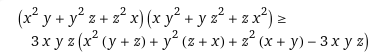
怎么证，好长好吓人关键是不知道如何用均值

记 `A=\sum x^2y`, `B=\sum xy^2`, `C=3xyz`, `D=\sum x^2(y+z)-3xyz`，注意到 `A+B=C+D`，故
\begin{align*}
AB\geqslant CD&\iff(A+B)^2-(A-B)^2\geqslant(C+D)^2-(C-D)^2\\
&\iff(C-D)^2\geqslant(A-B)^2,
\end{align*}左边配方右边分解，不等式变成
\[\left( \sum x(y-z)^2 \right)^2\geqslant\prod(y-z)^2,\]不妨设 `z=\min\{x,y,z\}`，令 `x=z+t`, `y=z+u`, `t`, `u\geqslant0`，上式即
\[\bigl( (z+t)u^2+(z+u)t^2+z(t-u)^2 \bigr)^2\geqslant t^2u^2(t-u)^2,\]显然有
\[\LHS\geqslant(tu^2+ut^2)^2=t^2u^2(t+u)^2\geqslant\RHS.\]