|
|
Last edited by hbghlyj 2021-1-31 11:50
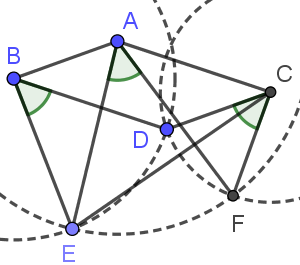
平行四边形ABCD,以A为中心,任意长为半径作圆,以B为中心过D作圆,以C为中心过D作圆,圆A与圆B交于E,圆A与圆C交于F,求证$\angle EAF=\angle EBD=\angle DCF$.
证:$\triangle BEA\cong\triangle CAF$(SSS)$\implies\angle EBD=\angle DCF\implies\triangle DBE\sim\triangle DCF\implies DE:DF=DB:DC=BE:BA$.
$\angle EDF=360^\circ-\angle BDE-\angle CDF-\angle BDC=(180^\circ-2\angle BDE)+(180^\circ-\angle BDC)=\angle DBE+\angle ABD=\angle ABE$⇒△DEF~△BEA⇒△AEF~△BED⇒∠EAF=∠EBD=∠DCF.
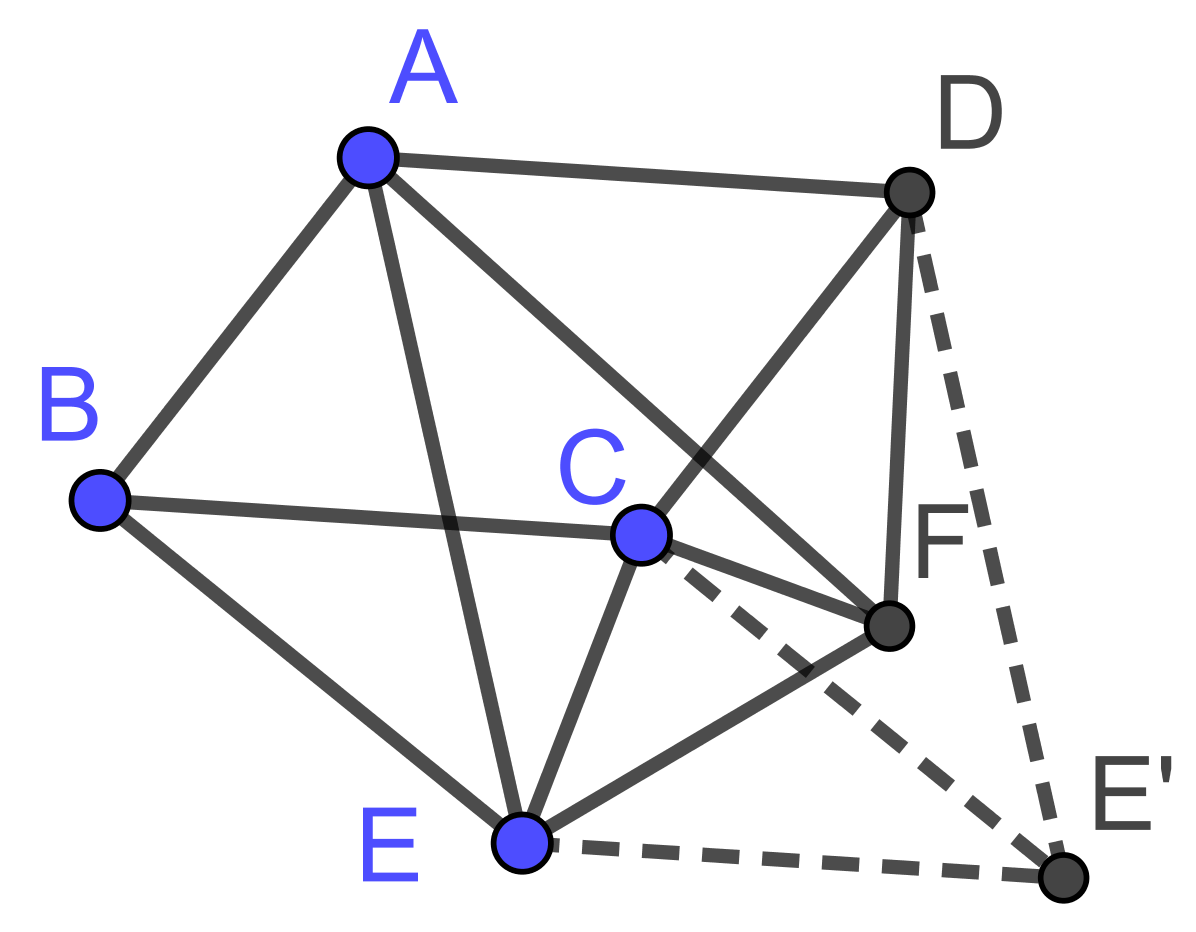
推广:以平行四边形ABCD的边BC和CD为边长向形外作两个相似三角形BEC与DCF,求证$\triangle AEF\sim\triangle BEC$.(例3.1.4.几何变换与几何证题)
作平移AD,则B→C,设$E\to E'$,则$\triangle DCE'\cong\triangle ABE,\triangle E'CE\sim\triangle DCF$.由于$\angle E'CE=\angle DCF$,所以$\angle E'CD=\angle ECF$.又$\frac{CE'}{CE}=\frac{DC}{CF}$,所以$\triangle DCE'\sim\triangle FCE.$但$\triangle DCE'\cong\triangle ABE$,所以$\triangle ABE\sim\triangle FCE$,于是$\frac{EA}{EB}=\frac{EF}{EC},\angle FEC=\angle AEB,$进而$\angle FEA=\angle CEB,$故$\triangle AEF\sim\triangle BEC.$
|
|