四点中每个点在过其余三点的圆内部

hbghlyj

不存在四个点,每个点在过其余三点的圆内部.
不存在四个点,每个点在过其余三点的圆外部.
不存在四个点A,B,C,D,点A在过B,C,D的圆外部,而且,除A外,每个点在过其余三点的圆内部.
-----------
验证:

2. f[a_List, b_List, c_List,d_List] = Tally[Table[
3.   g[{RandomReal[], RandomReal[]}, {RandomReal[],
4.     RandomReal[]}, {RandomReal[], RandomReal[]}, {RandomReal[],
5.     RandomReal[]}], 20000]]((Last[b] - Last[c]) (-First[a]^2 First[d] -
6.        First[d] (Last[a] - Last[b]) (Last[a] - Last[c]) +
7.        First[a] (First[
8.            d]^2 + (Last[b] - Last[d]) (Last[c] - Last[d]))) +
9.     First[c] (First[
10.          d]^2 (Last[a] -
11.           Last[b]) + (First[
12.            a]^2 + (Last[a] - Last[b]) (Last[a] - Last[d])) (Last[b] -
13.           Last[d])) +
14.     First[b]^2 (First[d] (Last[a] - Last[c]) +
15.        First[a] (Last[c] - Last[d]) + First[c] (-Last[a] + Last[d])) +
16.      First[c]^2 (First[d] (-Last[a] + Last[b]) +
17.        First[a] (-Last[b] + Last[d])) +
18.     First[b] (-(Last[a] - Last[c]) (First[
19.            d]^2 + (Last[a] - Last[d]) (Last[c] - Last[d])) +
20.        First[c]^2 (Last[a] - Last[d]) +
21.        First[a]^2 (-Last[c] + Last[d])))/(First[
22.       c] (Last[a] - Last[b]) + First[a] (Last[b] - Last[c]) +
23.     First[b] (-Last[a] + Last[c]));
24. g[a_List, b_List, c_List, d_List] = {f[b, c, d, a] > 0,f[a, c, d, b] > 0, f[a, b, d, c] > 0, f[a, b, c, d] > 0};
25. Tally[Table[
26.   g[{RandomReal[], RandomReal[]}, {RandomReal[],
27.     RandomReal[]}, {RandomReal[], RandomReal[]}, {RandomReal[],
28.     RandomReal[]}], 20000]]

Copy the Code

输出:
{{{False, False, True, True},2316},
{{False, True, True, False},2359},
{{False, True, True, True},1498},
{{False, True, False, True},2319},
{{True, False, True, False},2258},
{{True, True, True, False},1524},
{{True, True, False, True},1519},
{{True, False, True, True},1533},
{{True, True, False, False},2340},
{{True, False, False, True},2334}}
涵盖了10种情况,用0和1写出来是:
{{0,0,1,1},{0,1,1,0},{0,1,1,1},{0,1,0,1},{1,0,1,0},{1,1,1,0},{1,1,0,1},{1,0,1,1},{1,1,0,0},{1,0,0,1}}
也就是说,有2个1,2个0或者3个1,1个0的全部情况.分别画图说明如下:

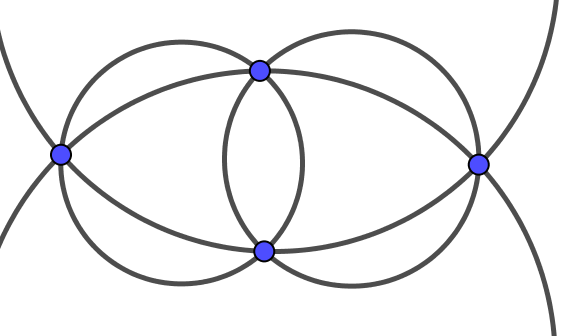
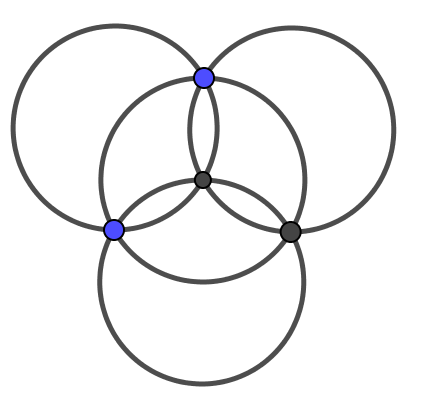
我们还有6个情况,它们都是不可能的:
4个1:{1,1,1,1}
1个1,3个0:{1,0,0,0},{0,1,0,0},{0,0,1,0},{0,0,0,1}
4个0:{0,0,0,0}

hbghlyj

1#的证明很简单.
这四个点,要么组成凸四边形,要么其中一个点在另外三个的三角形内部.
分别对应,2个1,2个0或者3个1,1个0的全部情况.
那么,再搞一下五个点.
过四个点能做一条抛物线.
重新做一遍