三个点分三个边的比相等.

hbghlyj

D,E,F在BC,CA,AB上,$\overline{BD}:\overline{DC}=\overline{CE}:\overline{EA}=\overline{AF}:\overline{FB}$.a,b,c为ABC的三边长,d,e,f为DEF的三边长.
求证:点D变化时,$\frac{d^2e^2+d^2f^2+e^2f^2}{d^4+e^4+f^4}$是定值.(这个定值有何几何意义呢 )
证:只需证(a²b²+a²c²+b²c²)(d⁴+e⁴+f⁴)=(d²e²+d²f²+e²f²)(a⁴+b⁴+c⁴).作代换
$k^2 b^2 + (1 - k)^2 c^2 - k (1 - k) (b^2 + c^2 - a^2) = d^2,$
$  k^2 c^2 + (1 - k)^2 a^2 - k (1 - k) (c^2 + a^2 - b^2) = e^2,$
$  k^2 a^2 + (1 - k)^2 b^2 - k (1 - k) (a^2 + b^2 - c^2) = f^2$
化简得(a²b²+a²c²+b²c²)(d⁴+e⁴+f⁴)-(d²e²+d²f²+e²f²)(a⁴+b⁴+c⁴)=0
注:
用这个结论可直接得出zhuanlan.zhihu.com/p/356581409.

其妙

回复 1# hbghlyj

不知道是不是类似题，因为你没画图，仅供参考，详见：mp.weixin.qq.com/s?__biz=MzIxMDYxMDMxOQ==& … 99&lang=zh_CN#rd

hbghlyj

回复 2# 其妙
我觉得不需要画图吧. 文字描述已经很精确了
没有看出联系...能否提示一下

hbghlyj

回复 2# 其妙
发现一个笔误

hbghlyj

回复 2# 其妙
找到原帖了forum.php?mod=viewthread&tid=5589

hbghlyj

下面来研究一下各种有趣的特殊情况
①{d,e,f}={a,b,c}
\[d^2+e^2+f^2-a^2-b^2-c^2=3 (k-1) k \left(a^2+b^2+c^2\right)\]所以只有平凡解k=0或1,也就是,两个三角形重合.
②d:e:f=a:b:c
从$d^2 b^2-e^2 a^2=d^2 c^2-f^2a^2=0$消去k得$a^4 + b^4 +c^4- a^2 b^2 - a^2 c^2 - b^2 c^2 =0$,故a=b=c.
③d:e:f=b:c:a
和②一样,也只有等边三角形满足.
④d:e:f=(b+c-a):(c+a-b):(a+b-c)
除等边三角形的情况外,还有\[30abcΣb^2c^2+18abcΣa^4+6Σb^2c^5+6Σb^5c^2+3Σa^7-5Σa^2b^2c^3-6Σb^3c^4-6Σb^4c^3-7Σbc^6-7Σb^6c-16Σab^2c^4-16Σab^4c^2=0\]但是后来发现这种情况是不存在的.为此,我们要证明,在三角形中,$30 a b c \left(a^2 b^2+a^2 c^2+b^2 c^2\right)-5 \left(a^3 b^2 c^2+a^2 b^2 c^3+a^2 b^3 c^2\right)+18 a b c \left(a^4+b^4+c^4\right)-6 \left(a^4 b^3+a^3 c^4+b^4 c^3\right)-16 \left(a^4 b^2 c+a^2 b c^4+a b^4 c^2\right)-16 \left(a^2 b^4 c+a^4 b c^2+a b^2 c^4\right)-6 \left(a^3 b^4+a^4 c^3+b^3 c^4\right)+6 \left(a^5 b^2+a^2 c^5+b^5 c^2\right)+6 \left(a^2 b^5+a^5 c^2+b^2 c^5\right)-7 \left(a^6 b+a c^6+b^6 c\right)-7 \left(a^6 c+a b^6+b c^6\right)+3 \left(a^7+b^7+c^7\right)<0$
作代换a=y+z,b=z+x,c=x+y后化为$-7 x^3 y^2 z^2-7 x^2 y^2 z^3-7 x^2 y^3 z^2-2 x^4 y^2 z+6 x^3 y^3 z-2 x^2 y^4 z-2 x^4 y^3-2 x^3 y^4-2 x^4 y z^2+6 x^3 y z^3-2 x^2 y z^4+6 x^5 y z+x^6 y-2 x^4 z^3-2 x^3 z^4+x^6 z-2 x y^2 z^4+6 x y^3 z^3-2 x y^4 z^2+6 x y^5 z+x y^6+6 x y z^5+x z^6-2 y^3 z^4-2 y^4 z^3+y^6 z+y z^6+x^7+y^7+z^7>0$
作代换$x =u + v + w, y =v + w, z = w$后化为
$48 w^5 \left(u^2+u v+v^2\right)+4 w^4 (u+2 v) \left(26 u^2+17 u v+17 v^2\right)+w^3 \left(533 u^2 v^2+382 u^3 v+87 u^4+302 u v^3+151 v^4\right)+3 w^2 (u+2 v) \left(63 u^2 v^2+50 u^3 v+13 u^4+26 u v^3+13 v^4\right)+w \left(187 u^4 v^2+258 u^3 v^3+169 u^2 v^4+66 u^5 v+9 u^6+48 u v^5+16 v^6\right)+u^2 (u+2 v) \left(u^2+3 u v+3 v^2\right)^2>0$

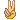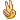
取等条件是u=w=0或u=v=0,所以原不等式的取等条件为a:b:c=1:1:1或2:1:1