立体几何难起来 真的堪比蜀道

facebooker

超级难 题目都没看懂 帮忙分析一下吧

kuing

难在一条直线与四条异面直线相交不太好想象。

那先不管 `BE`，只看另外三条，也就是下图中的三条蓝色线，我们就来作一条直线与这三条蓝线相交。



如图，在 `AC_1` 上任取一点 `P`，`D_1P` 交 `AB` 于 `Q`，过 `Q` 作 `AD` 的平行线交 `CD` 于 `R`，显然 `RP` 将与 `D_1A_1` 相交，记交点为 `S`，所以红线 `RS` 就是与三条蓝线相交的直线。

由于 `P` 是任取的，所以这样的红线有无数条。

现在再看回 `BE`，由于 `BE` 要与这条红线 `RS` 相交，那么 `E` 就必须在平面 `BRS` 与底面 `A_1B_1C_1D_1` 的交线上，我们把这条交线作出来，也很简单，如下图，`BP` 交 `C_1D_1` 于 `T`，那么 `ST` 就是所求交线，也就是说 `E` 得在绿线 `ST` 上。



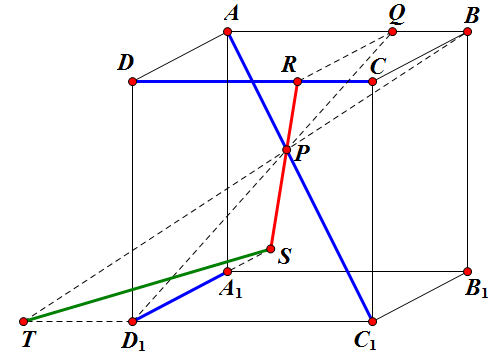
这图开头的 `P` 取得太随便，结果绿线在底面正方形之外了，把 `P` 往下移一下，绿线就会进去了，我就不重画了。

现在来看看这条绿线有啥特别，注意到 `SD_1:RQ = D_1P:PQ = TC_1:AB`，可见 `SD_1 = TC_1`，所以如果在底面建坐标系，以 `D_1` 为原点，`D_1C_1` 为 `x` 轴，`D_1A_1` 为 `y` 轴，设 `T(a,0)`，则 `S(0,m-a)`，故 `ST` 的方程就是 `x/a+y/(m-a)=1`，当 `0<a<m` 且 `x`, `y` 为正时，它们就是题目中那两个 `d`，于是由柯西不等式有 `m = (a+m-a)[x/a+y/(m-a)] \geqslant (\sqrt x+\sqrt y)^2`，即 `\sqrt x+\sqrt y\leqslant\sqrt m`，所以选 D。