来自人教群——两球半径之和最大值

kuing

鄂B爱好者羽林(3086*****) 2021/5/10 11:19:16
在长方体$ABCD{-}A_1B_1C_1D_1$中，AB=13，AD = 5，$AA_1= 12$，过点$A$且与直线CD平行的平面$\alpha$将长方体分成两部分。现同时将两个球分别放入这两部分几何体内，则在平面$\alpha$变化的过程中,这两个球的半径之和的最大值为

由于 `AB` 足够长，所以可以转化为平面问题：

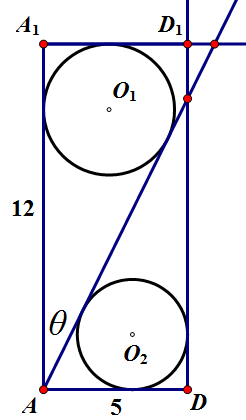
如图，过 `A` 的直线将矩形 `ADD_1A_1` 分成两部分，求两部分内的两圆之和的半径最大值。

设直线与 `AA_1` 夹角为 `\theta`，当 `\theta` 还没大到圆 `O_1` 碰到 `DD_1` 之前，有
\begin{align*}
r_1+r_2&=12\cdot\frac{1+\tan\theta-\sec\theta}2+5\cdot\frac{1+\cot\theta-\csc\theta}2\\
&=\frac{17}2+6\cdot\frac{\sin\theta-1}{\cos\theta}+\frac52\cdot\frac{\cos\theta-1}{\sin\theta}\\
&=\frac{17}2-6\tan\left( \frac\pi4-\frac\theta2 \right)-\frac52\tan\frac\theta2\\
&=f(\theta),
\end{align*}求导得
\[f'(\theta)=3\sec^2\left( \frac\pi4-\frac\theta2 \right)-\frac54\sec^2\frac\theta2,\]而当 `\theta<\pi/2` 时有
\[\cos\left( \frac\pi4-\frac\theta2 \right)=\frac1{\sqrt2}\left( \cos\frac\theta2+\sin\frac\theta2 \right)<\sqrt2\cos\frac\theta2,\]所以
\[f'(\theta)>\frac32\sec^2\frac\theta2-\frac54\sec^2\frac\theta2>0,\]所以此时半径之和关于 `\theta` 递增。

而当 `\theta` 大到圆 `O_1` 碰到 `DD_1`，`r_1` 便不能再大，而 `r_2` 减少，所以半径之和由此开始减少，亦即当圆 `O_1` 刚碰到 `DD_1` 时半径之和最大。

具体值懒得算了……

isee

如果这两个球一样大，最大半径的时候岂不是就是体对角面时？

kuing

回复 2# isee

最大不是两球一样大的时候啊，你难道没看懂我的过程……

isee

回复 3# kuing

说的如果，知道原题并不是等球

kuing

回复 4# isee

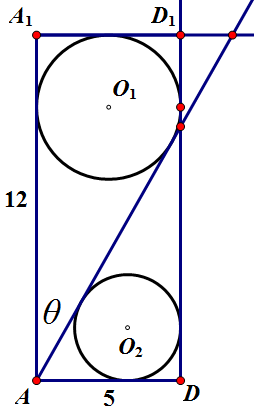
哦，你是说规定让他们一样大，那就没难度了啊，即是让较小部分的内切最大，当然是对角面的时候了