|
|
Last edited by hbghlyj 2022-8-19 22:43
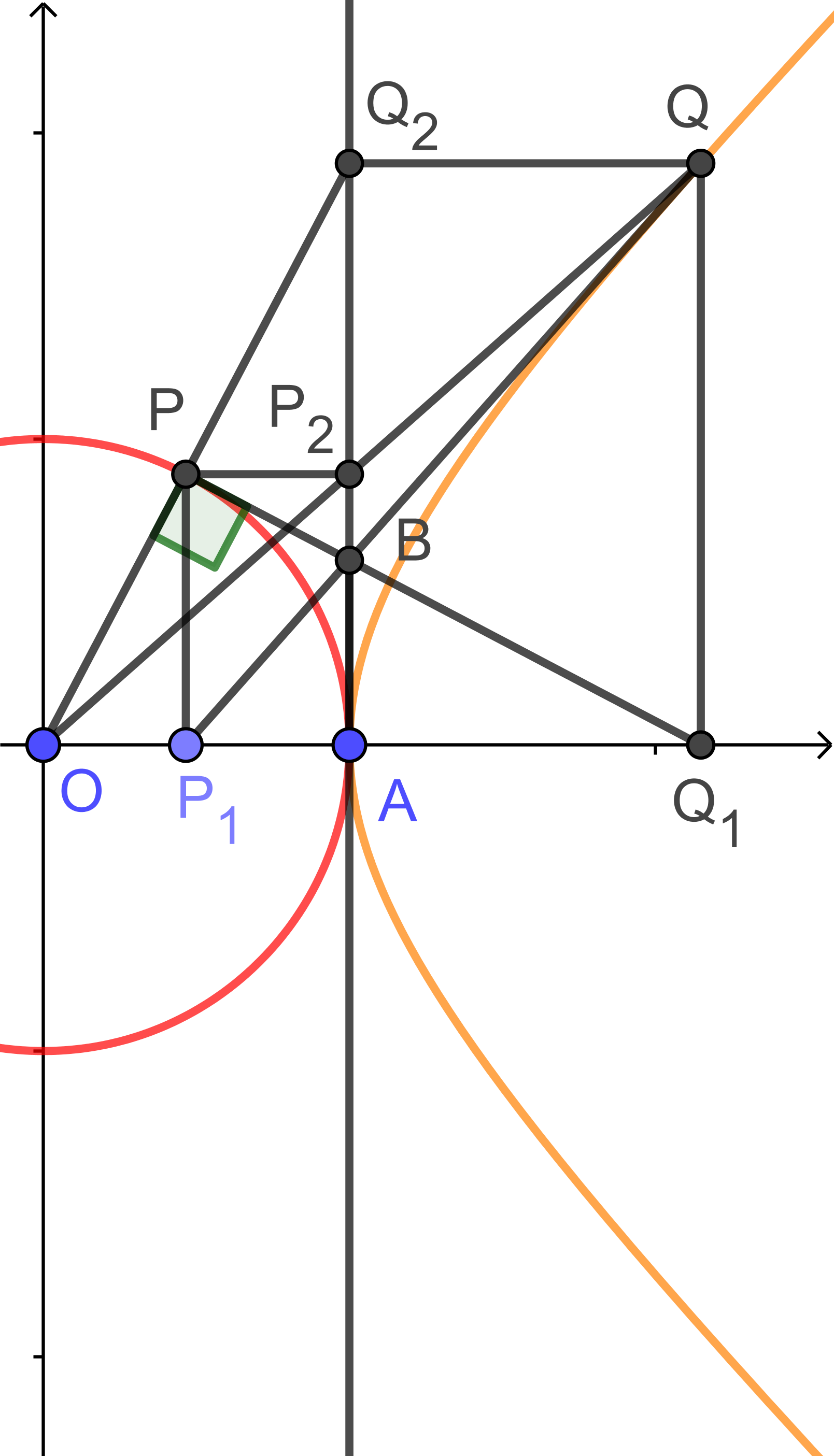
| $c:x^2+y^2=1$上的点$P$,经过如下映射$f$到$d:x^2-y^2=1$上的点$Q$: |
⑴$P$投影到$x$轴上的点$P_1$,过$P$作$c$的切线交$x=1$于$B$,交$x$轴于$Q_1$,过$Q_1$作$x$轴的垂线交$BP_1$于$Q$.
反过来,$Q$投影到$x$轴上的点$Q_1$,过$Q$作$d$的切线交$x=1$于$B$,交$x$轴于$P_1$,过$P_1$作$x$轴的垂线交$BQ_1$于$P$.
⑵$P$投影到$x=1$上的点$P_2$,$OP_2$与$d$交于$Q$;反过来,$Q$投影到$x=1$上的点$Q_2$,$OQ_2$与$c$交于$P$.
⑶$(x_Q,y_Qi)$是$PP_1$与$d$的交点;反过来,$(x_P,y_Pi)$是$QQ_1$与$c$的交点.
⑷$x_Px_Q=1,\frac{y_Q}{y_P}-\frac{y_P}{y_Q}=1$,$PQ$经过$(-1,0)$.
⑸$y_Q=\frac{y_P}{x_P},y_P=\frac{y_Q}{x_Q}$
因此,若把$f$的定义域视为圆和双曲线之并,则$f$的逆映射为自身,即$f=f^{-1}$.
把$f$扩展到整个复平面上,则有:\[f(z)=\frac{z-\overline{z}+2}{z+\overline{z}}\]然后验证一下:\[f(f(z))=\frac{\frac{z-\overline{z}+2}{\overline{z}+z}-\frac{\overline{z}-z+2}{\overline{z}+z}+2}{\frac{z-\overline{z}+2}{\overline{z}+z}+\frac{\overline{z}-z+2}{\overline{z}+z}}=z\]果然是成立的.$f$的定义域就是复平面去掉虚轴,即$\mathbb C-i\mathbb R$.另外,$z$和$f(z)$的连线经过$(-1,0)$.
对称性 $f(z)$是关于原点对称,$x,y$轴对称的函数.
不动点 由$f(z)=z$化简得$(z+1)(z+\overline{z}-2)=0$,因此$f$的不动点为$-1$并上直线$x=1$.
直线的像 显然,任何直线的像为直线.
由$\forall a,b\in\mathbb C:a\ f(z)+ b\ \overline{f(z)}- 1=k(a z+b\overline{z}-1)$得$a+b= -1$或$a=b= \frac{1}{2}$
因此,直线$ty-x=1$和$x=1$的像为自身,其中$t$是任意实数.
抛物线$y=x^2$的像为$y=\frac1x$,原点被映射到$x$轴上的无穷远点. |
|