(学为点晴卷)数列压轴题

hao124

数列$\an$，已知$a_1∈(\frac{1}{2},1),\ln a_{n+1}=a_n-\ln a_n-2$，求证$\frac{1}{e}<a_{2021}<\frac{2}{e}$

realnumber

用几何画板试验了下,大约$a_1\in (0.03,5.3)$时,$a_n$4,5项后 就在0.4639附近了(即$y=x^2$与$y=e^{x-2},x>0$交点横坐标)
$a_1$不在这个范围似乎就发散了
             设$x_0$是方程$x^2=e^{x-2},x>0$的根,约为0.46392.
如图可得如下结论成立:若$a_n>x_0,则a_{n+2}<a_n$;若$a_n<x_0,则a_{n+2}>a_n$----(*)
\[ a_{n+2}=\frac{1}{a_{n+1}}e^{a_{n+1}-2}=\frac{a_n}{e^{a_n-2}e^{\frac{1}{a_n}e^{a_n-2}-2}}<a_n \iff \frac{1}{a_n}e^{a_n-2}-2<a_n-2   \iff e^{a_n-2}<a_n^2 \]



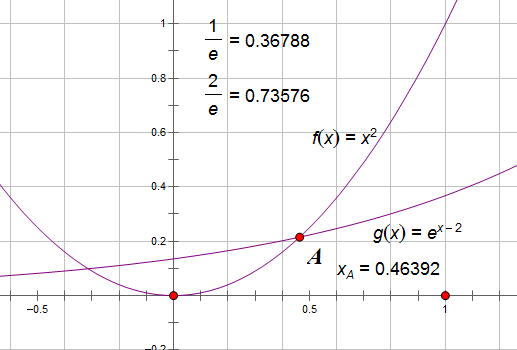
若$a_1=1$,得$a_2=\frac{1}{e},a_3\in (\frac{1}{e},\frac{2}{e})$,由(*),可得n>2时,都有$a_n\in  (\frac{1}{e},\frac{2}{e})$.

可能上面适当放缩一下可以得到$a_n$收敛于$x_0$的速度,比如考察$\frac{a_{n+2}-a_{n+1}}{a_n-a_{n-1}}<?$,应该不会慢的.