等轴双曲线 正方形

hbghlyj

守夜冠军

P是等轴双曲线上一点,过P的切线交两条渐近线于Q和R,易见PQ=PR.
QR的中垂线分别交x轴和y轴于A和B.
QR交y轴于E.
双曲线的焦距为2c.
求证:
AB=QR
BO⋅OE=c²

kuing

守夜冠军
ellipse 发表于 2021-5-31 04:54

这条双曲线只是提供了垂直和中点，其余没啥用，用完赶紧擦掉，变成纯几何：

如图，由中垂线知 `AQ=AR`，又 `\angle QOA=\angle ROA=45\du`，故 `\angle OQA` 与 `\angle ORA` 要么相等要么互补，如果相等就是 `P` 在 `OA` 上了，显然一般情况都不在，所以是互补的，这样就得到 `\angle QAR=90\du`，同理 `\angle QBR=90\du`，所以那就是正方形。

然后由 `\angle BOQ=\angle BQE=45\du` 得 `\angle BQO=\angle E`，那么 `\triangle BOQ\sim\triangle ROE`，从而 `OB\cdot OE=OQ\cdot OR`，回到双曲线上，易知这个 `OQ\cdot OR` 就是 `c^2`。

hbghlyj

推广:P是双曲线上一点,P处的法线与x轴,y轴分别交于Q,R,则PQ/PR为定值.
这个也有纯几何证明吗

hbghlyj

回复 3# ellipse
引理1.圆锥曲线的几何性质 命题11

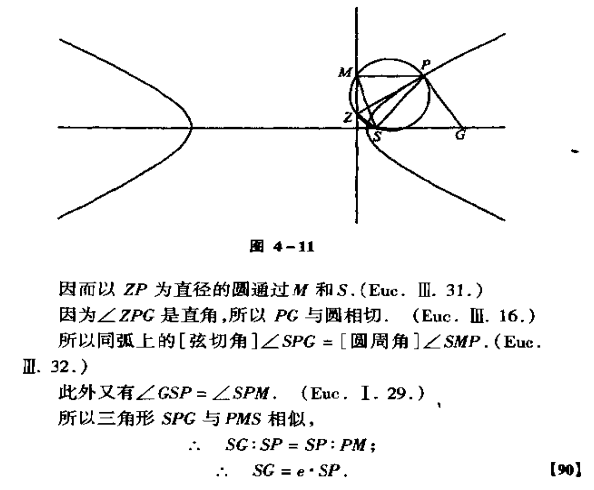
引理2.设S,S’是双曲线的右,左焦点,BP是法线,B在虚轴上,过P作实轴平行线交右准线于A,则BAS共线

证:设C是P处的切线与右准线AE的交点,D是PC与虚轴交点,由命题12有CP平分SPS',而SD=S'D,所以SS'DP共圆,又BP⊥PD,所以SS'BDP共圆,故∠CAS=∠CPS=∠DBS,因此BAS共线.
------
$\frac{BP}{BG}=\frac{AP}{SG}=\frac{AP}{SP}\frac{SP}{SG}=\frac1{e}\frac1{e}=\frac1{e^2}=\frac{a^2}{c^2}$
所以$\frac{BP}{PG}=\frac{a^2}{b^2}$