|
|
Author |
hbghlyj
Posted 2021-5-31 18:19
回复 4# 青青子衿
此答案准备用代数方法暴力统一通过坐标旋转，总可以使得圆锥曲线的对称轴平行于坐标轴，从而得圆锥曲线方程的一般形式：
$f(x, y)=a_{1} x^{2}+a_{2} y^{2}+a_{3} x+a_{4} y+a_{5}=0\,\,\left(a_{1} a_{2} \neq 0\right) \\$
设经过定点 $F (x_{0}, y_{0} )$ 的直线 $m$ 方程为
$x=x_{0}+t \cos \alpha,\,\,y=y_{0}+t \sin \alpha \\$
代入上式整理得
$\begin{aligned} &\left(a_{1} \cos ^{2} \alpha+a_{2} \sin ^{2} \alpha\right) t^{2}+\left[\left(2 a_{1} x_{0}+a_{3}\right) \cos \alpha+\left(2 a_{2} y_{0}+a_{4}\right) \sin \alpha\right] t+f\left(x_{0}, y_{0}\right)=0 \end{aligned}\tag 1\\$
设该直线与二次曲线 $f(x, y)=0$ 的交点为 $E ，D$，则由参数的几何意义得
$F E \cdot F D=t_{1} t_{2}=\frac{f\left(x_{0}, y_{0}\right)}{a_{1} \cos ^{2} \alpha+a_{2} \sin ^{2} \alpha} \\$
$(1)a_{1}=\frac{1}{a^{2}}, a_{2}=\frac{1}{b^{2}}, a_{3}=a_{4}=0, a_{5}=-1 \\$
则
$f(x, y)=\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-1=0 \\$
为椭圆方程。设经过椭圆中心 $O(0,0)$ 且与直线 $m$ 平行的直线与椭圆的交点为 $K,L$，则
$\begin{aligned} O K^{2}&=-O K \cdot O L\\ &=-\frac{f(0,0)}{a_{1} \cos ^{2} \alpha+a_{2} \sin ^{2} \alpha}\\ &=\frac{1}{a_{1} \cos ^{2} \alpha+a_{2} \sin ^{2} \alpha} \end{aligned}\\$
所以
$\begin{aligned} \frac{F E \cdot F D}{O K^{2}}&=f\left(x_{0}, y_{0}\right)=\frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}-1 \end{aligned}\\$
$(2)$$a_{1}=a_{2}=\frac{1}{r^{2}}, a_{3}=a_{4}=0, a_{5}=-1 \\$
则
$f(x, y)=\frac{x^{2}}{r^{2}}+\frac{y^{2}}{r^{2}}-1=0 \\$
为圆方程，此时
$\frac{F E \cdot F D}{O K^{2}}=\frac{F E \cdot F D}{r^{2}}=f\left(x_{0}, y_{0}\right), \\$
即
$F E\cdot F D=x_{0}^{2}+y_{0}^{2}-r^{2} \\$
$(3)$$a_{1}=\frac{1}{a^{2}}, a_{2}=-\frac{1}{b^{2}}, a_{3}=a_{4}=0, a_{5}=-1 \\$
则
$f(x, y)=\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}-1=0 \\$
为双曲线方程。设经过双曲线中心 $O(0,0)$ 且与直线 $m$ 平行的直线与双曲线的交点为 $K,L$，则
$\begin{aligned} O K^{2}&=-O K \cdot O L\\ &=-\frac{f(0,0)}{a_{1} \cos ^{2} \alpha+a_{2} \sin ^{2} \alpha}\\ &= \frac{1}{a_{1} \cos ^{2} \alpha+a_{2} \sin ^{2} \alpha} \end{aligned} \\$
所以
$\frac{F E \cdot F D}{O K^{2}}=f\left(x_{0}y_{0}\right)=\frac{x_{0}^{2}}{a^{2}}-\frac{y_{0}^{2}}{b^{2}}-1 \\$
$(4)$$a_{1}=0, a_{2}=\frac{1}{2 p}\,\,(p>0), a_{3}=-1,a_{4}=a_{5}=0 \\$
则
$f(x, y)=\frac{y^{2}}{2 p}-x=0 \\$
为抛物线方程，其对称轴为 $x$ 轴，顶点为原点。由 $(1)$式得
$\begin{aligned} F E \cdot F D&=t_{1} t_{2}=\frac{f\left(x_{0}, y_{0}\right)}{a_{2} \sin ^{2} \alpha}\\ &=\frac{\frac{y_{0}^{2}}{2 p}-x_{0}}{a_{2} \sin ^{2} \alpha} \\ t_{1}+t_{2}&=-\frac{-\cos \alpha+\frac{y_{0}}{p} \sin \alpha}{a_{2} \sin ^{2} \alpha} \end{aligned} \\$
设经过抛物线焦点$ S\left(\frac{p}{2}, 0\right)$ 且与直线 $m$ 平行的直线与抛物线交点为 $P, Q$ ，则
$\begin{aligned} l&=|P Q|=\left|t_{1}-t_{2}\right| \\ & =\sqrt{\left(t_{1}+t_{2}\right)^{2}-4 t_{1} t_{2}} \\ & =\sqrt{\left(-\frac{-\cos \alpha}{a_{2} \sin ^{2} \alpha}\right)^{2}-\frac{-2 p}{a_{2} \sin ^{2} \alpha}} \\ & =\frac{1}{a_{2} \sin ^{2} \alpha} \\ \end{aligned} \\$
所以
$\frac{F E \cdot F D}{l}=f\left(x_{0}, y_{0}\right)=\frac{y_{0}^{2}}{2 p}-x_{0} \\$
$(5)$$a_{1}=0, a_{2}=\frac{1}{2 p}(p>0), a_{3}=1,a_{4}=a_{5}=0 \\$
则
$f(x, y)=\frac{y^{2}}{2 p}+x=0 \\$
为抛物线方程，其对称轴为 $x$ 轴，顶点为原点，此时
$\frac{F E \cdot F D}{l}=f\left(x_{0}, y_{0}\right)=\frac{y_{0}^{2}}{2 p}+x_{0} \\$
综上可知，圆锥曲线幂可以有统一的代数表达形式
再补点
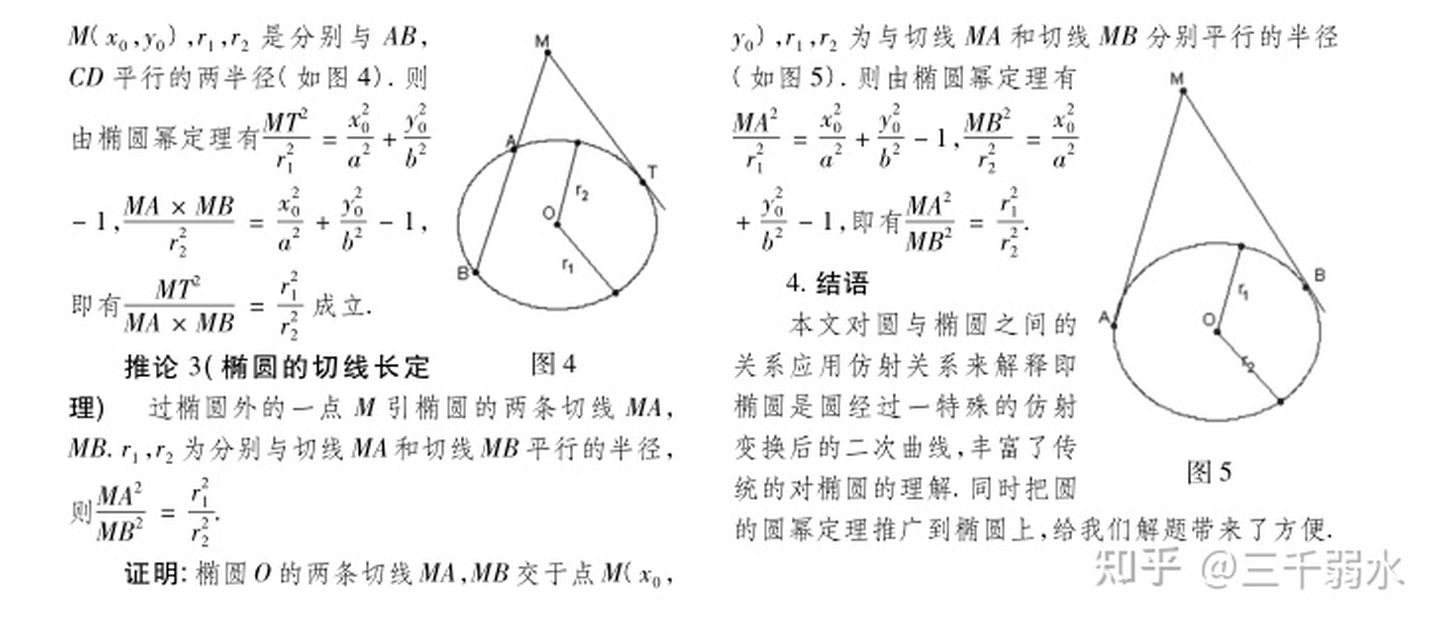
参阅
[1]陈波.从圆幂定理到圆锥曲线幂定理[J].数学教学,2016(5):42-45.
[2]谢玉兰.圆幂定理在椭圆上的推广及其若干推论[J].中学数学研究,2018(8):26-27.
直观感受一下
想办法用射影变换往圆上靠
由于一条线段的长度在射影变换下并不是线性变化的(除了特殊情况)，那如果我们想找不变量的话就需要引入另一个量，这就是与这条线段平行的椭圆半径
然后可以发现射影变换下他们的长度都成比例，然后就想通了
|
|
kuing
Posted 2021-5-31 17:54
青青子衿
Posted 2021-5-31 18:13
isee
Posted 2021-5-31 19:30
