凹蚶線

hbghlyj

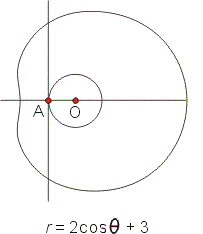
上圖顯示蚶線 $r= 2\cos \theta +3$。 在左側部分，呈「凹入」的現象，但這不是普遍現象。 事實上，當 2a < k < 4a 時，蚶線 $r=2a\cos\theta+k$ 有凹入現象，稱為凹蚶線； 但當 $k \leq 4a$ 時，蚶線 $r=2a\cos\theta+k$ 就不再有凹入現象了， 稱為凸蚶線。
——引自这里

如何证明「凹、凸的分別在於 k 是否大於 4a」呢
非常简单.$f(\theta )=2 a \cos ^2\theta +k \cos \theta $,则$f^{\prime\prime}(\pi )=-4 a + k$.