两正方形求证顶点距离平方和等式

hbghlyj

ABCD,EFGH是同向正方形,求证\[AE^2-BF^2+CG^2-DH^2=0\]

kuing

设两正方形的中心分别为 `O_1`, `O_2`，并记 `AO_1=a`, `EO_2=b`, `O_1O_2=c`，则
\begin{align*}
AE^2&=\bigl(\vv{AO_1}+\vv{O_1O_2}+\vv{O_2E}\bigr)^2\\
&=a^2+b^2+c^2+2\vv{AO_1}\cdot\vv{O_2E}+2\vv{O_1O_2}\cdot\bigl(\vv{AO_1}+\vv{O_2E}\bigr),
\end{align*}其余同理，故
\begin{align*}
&\frac{AE^2-BF^2+CG^2-DH^2}2\\
={}&\vv{AO_1}\cdot\vv{O_2E}-\vv{BO_1}\cdot\vv{O_2F}+\vv{CO_1}\cdot\vv{O_2G}-\vv{DO_1}\cdot\vv{O_2H}\\
&+\vv{O_1O_2}\cdot\bigl(\vv{AO_1}+\vv{O_2E}-\vv{BO_1}-\vv{O_2F}+\vv{CO_1}+\vv{O_2G}-\vv{DO_1}-\vv{O_2H}\bigr),\\
={}&\vv{AO_1}\cdot\vv{O_2E}-\vv{BO_1}\cdot\vv{O_2F}+\vv{CO_1}\cdot\vv{O_2G}-\vv{DO_1}\cdot\vv{O_2H},
\end{align*}由于 `\vv{BO_1}` 和 `\vv{O_2F}` 分别为 `\vv{AO_1}` 和 `\vv{O_2E}` 同方向旋转 `90\du` 而来，故必有 `\vv{AO_1}\cdot\vv{O_2E}=\vv{BO_1}\cdot\vv{O_2F}`，同理 `\vv{CO_1}\cdot\vv{O_2G}=\vv{DO_1}\cdot\vv{O_2H}`，从而得出 `AE^2-BF^2+CG^2-DH^2=0`。

而且由上述证明可以发现，两个正方形其实可以改成两个相似的矩形，结论同样成立。

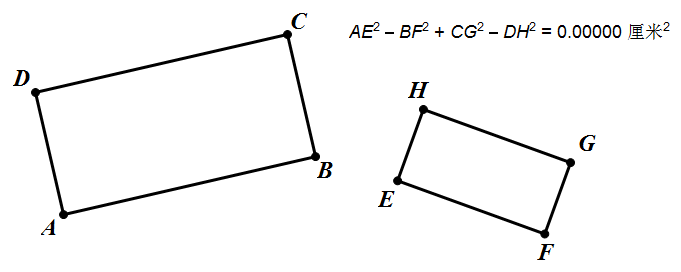
这样一来，这命题就可以看作是“`PA^2+PC^2=PB^2+PD^2`”这个结论的推广了。

isee

回复 2# kuing


这些题风格夸度颇大，你切换自如啊，