格雷贝定理

hbghlyj

在$△A_1A_2A_3$的外侧作正方形$A_2A_3P_1Q_1,A_3A_1P_2Q_2,A_1A_2P_2Q_2$.设$P_2Q_2$与$P_3Q_3,P_3Q_3$与$P_1Q_1$,$P_1Q_1$与$P_2Q_2$的交点依次为$B_1,B_2,B_3$,则$B_1A_1,B_2A_2,B_3A_3$三线共点.

kuing

？？三线共点这不是显然的吗？
而且不需要什么作正方形，只要三边分别平行，就一定共点啊，共的就是位似中心啊……

isee

回复 2# kuing

"格雷贝定理"，楼主应该是大意了，共点是绝对的，可能要证，这个点是某种特殊点，如五心之类的东西，不过，肯定是五心之外的心

kuing

回复 3# isee

一看就是到三边距离之比等于三边长之比的那个点（我不知道这点叫什么……

isee

回复 4# kuing


  baike.baidu.com/item/格雷贝作图法/18895874

isee

回复 4# kuing


还真是，《几何瑰宝-平面几何500名题暨1000条定理(上)》 ，第288页，这样的点叫共轭重心

hbghlyj

直接计算重心坐标应很简单

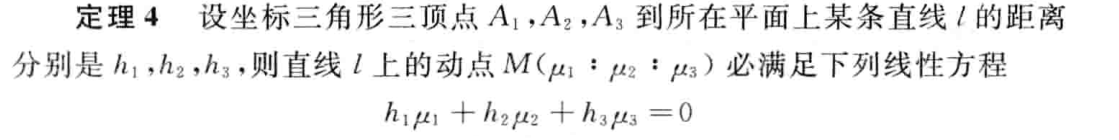
所以$P_1Q_1,P_2Q_2,P_3Q_3$的方程为$$ \left(h_{1}+a_{1}\right) \mu_{1}+a_{1} \mu_{2}+a_{1} \mu_{3}=0 $$$$ a_{2} \mu_{1}+\left(h_{2}+a_{2}\right) \mu_{2}+a_{2} \mu_{3}=0 $$$$ a_{3} \mu_{1}+a_{3} \mu_{2}+\left(h_{3}+a_{3}\right) \mu_{3}=0 $$其中,$h_1,h_2,h_3$分别表示各对应边上的高,据此可求出$P_2Q_2,P_3Q_3$交点$B_1$的坐标$$ B_{1}=\left(h_{2} h_{3}+a_{2} h_{3}+a_{3} h_{2}:-a_{2} h_{3}:-a_{3} h_{2}\right) $$于是直线$B_1A_1$的方程是$ a_{3} h_{2} \mu_{2}=a_{2} h_{3} \mu_{3} $显然共轭重心K=$ \left(a_{1}^{2}: a_{2}^{2}: a_{3}^{2}\right) $满足此方程.