垂足圆与一边相切

hbghlyj

第一题:
若P点关于△ABC的垂足圆⊙O恰与BC相切，ABCD是等腰梯形，I是△ABC的内心，过O、I作BC的平行线及垂线围成矩形OEIF。求证：D、E、F三点共线。

第二题:
若P点关于△ABC的垂足圆恰与BC相切于D，其半径为r，AH是BC边上的高。
求证：$(\mathrm{AH}-\mathrm{r})(\mathrm{BD}-\mathrm{CH})=\frac{\mathrm{AB}^{2}-\mathrm{AC}^{2}}{ \mathrm{BC}^2} \cdot \mathrm{S}_{\triangle \mathrm{ABC}}$

来自纯几何吧1927的43楼

hbghlyj

第一题的证明:
(当然,以下所设的字母D,E,F均与主楼第一题相同,与主楼第二题不同)

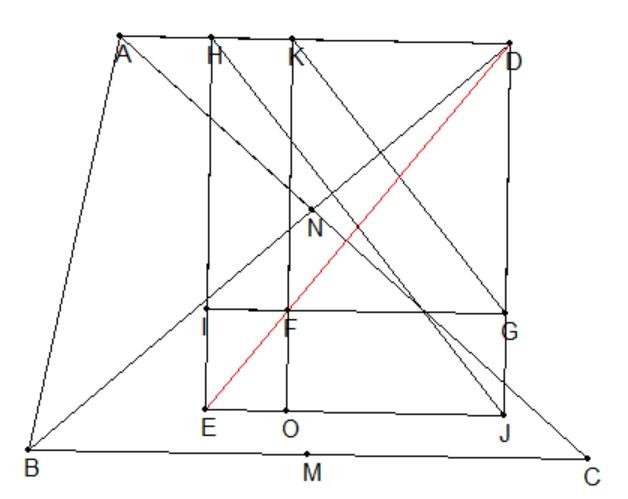
过D作AD垂线L，I在L和AD上的投影为G,H，O在L和AD上的投影为J,K，由第二题知DG⋅DH=DJ⋅DK，所以GK∥HJ，由FGK和EJH位似得DEF共线.
(从第二题推出，O的轨迹是以AD,L为渐近线且过I的双曲线，由定义不难看出它是BC垂线向的无穷远点的主等角曲线)

hbghlyj

但是...第二题如何证明呢