Last edited by hbghlyj 2021-6-16 05:21六边形ABCDEF的边的交错和为0⇔过A作BF垂线,过C作BD垂线,过E作DF垂线,三线共点⇔过B作AC垂线,过D作CE垂线,过F作EA垂线,三线共点.
①当六边形退化为三角形时(每条边是六边形的两条边),所共的两个点是等角共轭点.
(见几何瑰宝上册55-57页<共点线的施坦纳定理>:设A',B',C′分别是△ABC边BC,CA,AB上的一点,则过各点垂直于所在边的三条垂线共点的充要条件是六边形BA′CB′AC′的边的交错和等于0)
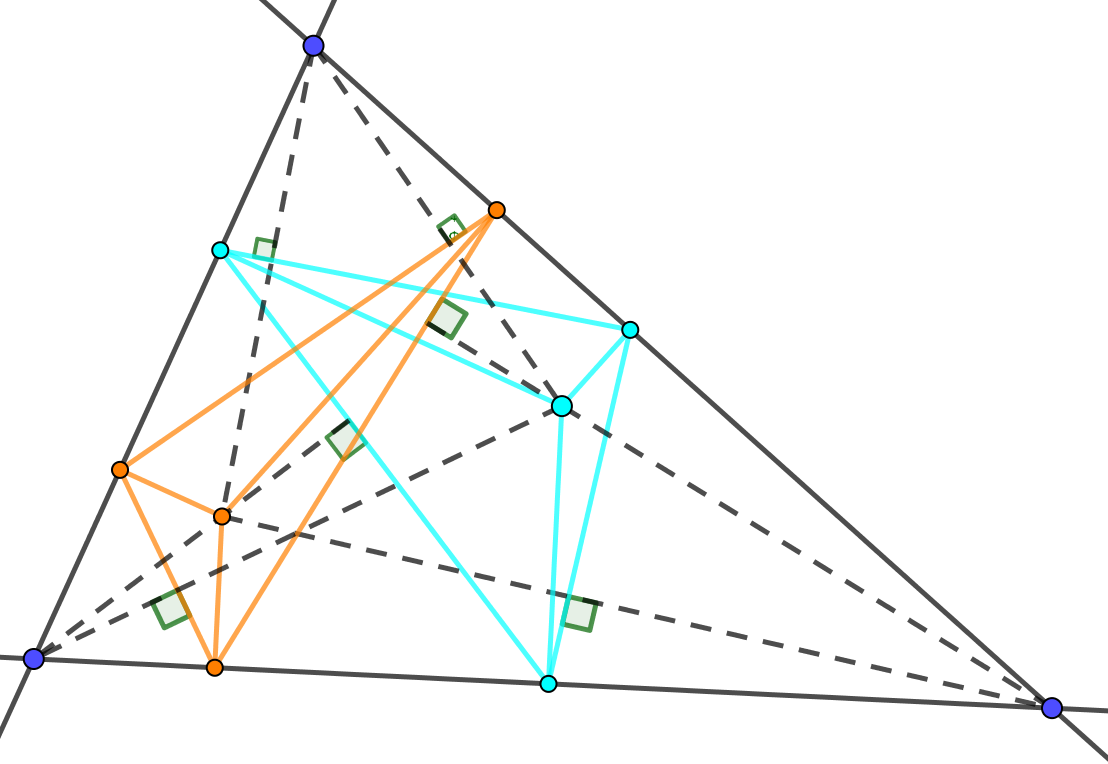
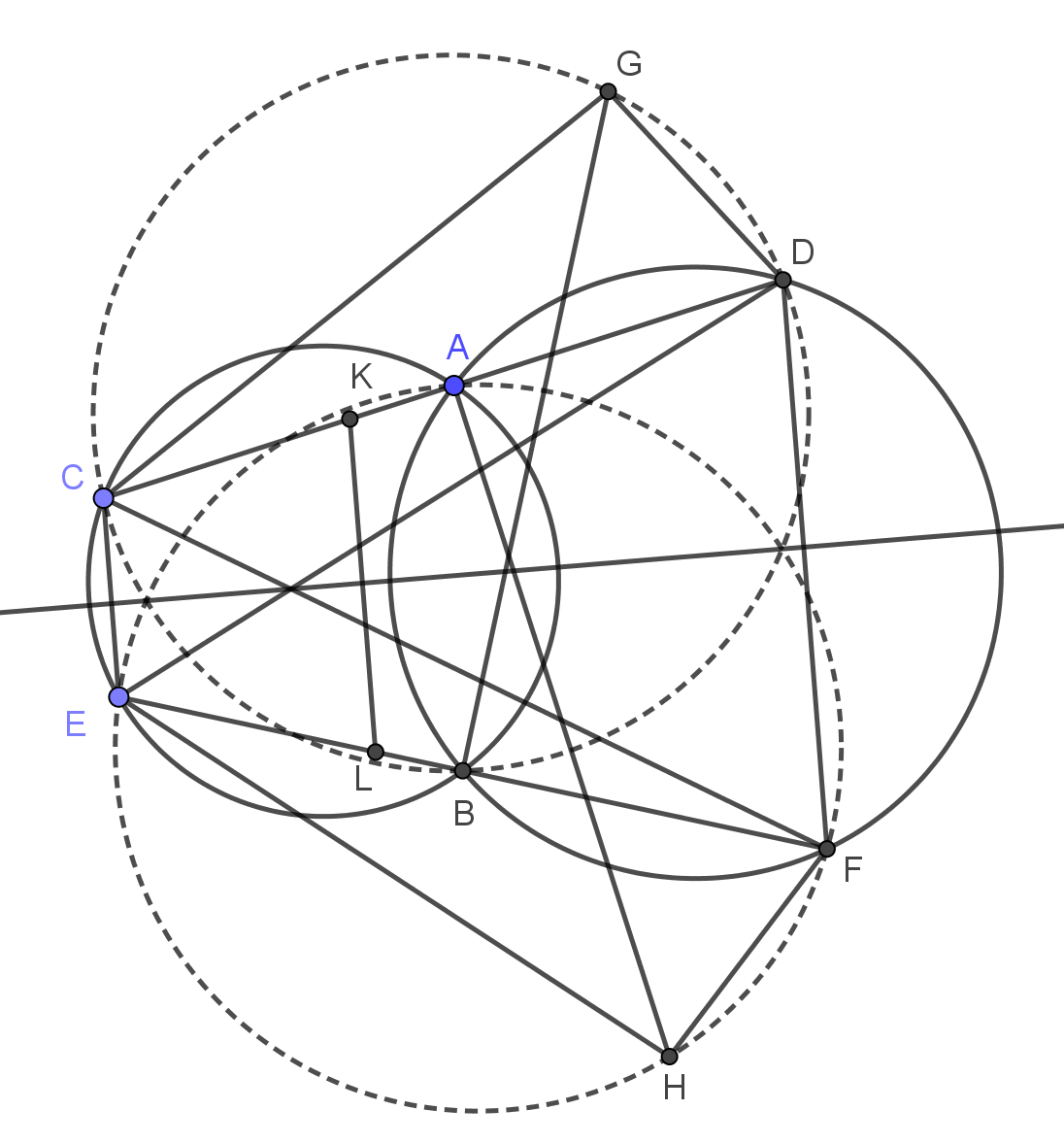
②在1#的图形中对于退化六边形(折四边形)CADEBF,得到:
过A作CD垂线,过E作BD垂线,过F作BC垂线,三线共点.
过B作EF垂线,过C作AF垂线,过D作AE垂线,三线共点.
此外还有一些性质:
△CDG与△EFH反相似.
△CDG关于BEF的垂极点K在CD上,△EFH关于ACD的垂极点L在EF上,KL与CE,DF平行.
进一步有AEFH,BCDG共圆,两圆的根轴通过CF和DE的交点且⊥CE.
③ABCD是直角梯形,∠ABC=∠BCD=90°,则六边形AEDBFC的交错和等于0(是②的特殊情况),F是△ADH关于BCF的垂极点,I是△BCG关于ADE的垂极点,FI∥AB∥CD.
另外,六边形AEDBFC满足$BF^2-CF^2-CD^2+DE^2-AE^2+AB^2=0$(不是交错和相等,符号有不同),使用这个轮换相加可以证明垂极点的存在性(见几何瑰宝上册55-57页<共点线的施坦纳定理>的推论)
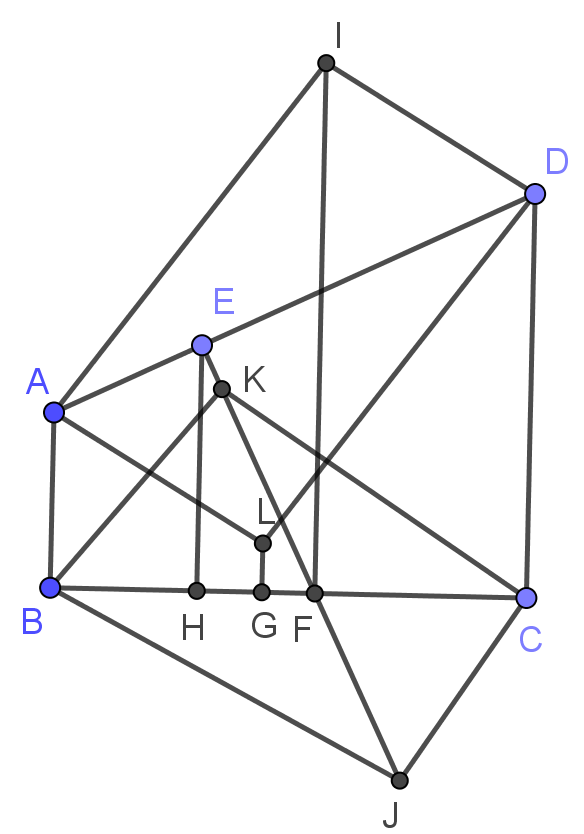
既然符号有不同,我们微调一下顺序:令G为F关于BC中点的对称点,则六边形AEDCGB的边的交错和相等,就产生了点K,L.(然而没有什么用)
顺便补充一下几何瑰宝:正交三角形定理就是书中排在它前面的马克斯维尔定理中一个三角形旋转90°而得,当然也可以用赛瓦定理证明. |
