一个三角形唯一 性问题

力工

这道题是不是解答有问题。
（1）过程中没用到三角形唯一存在；
(2)$BD$的下界没求出，就判断只选$BCD$.
求帮助，


怎样解才不罗里罗唆的。 我的想法是以A,D作圆，两圆在AC的左侧有交点D，这时三角形肯定唯一。

kuing

写这个答案的人根本就没有理解这道题，只是照以往求对角线最大值的方法写了一通企图蒙混过关，根本就不知道为什么会有一解二解。

显然从几何轨迹角度来看才简单，如图，固定 CD，A 在圆上动，易知 △ABC 是 60°Rt△，故 B 的轨迹也是圆且圆心 E 与 C、D 也构成 60°Rt△，圆半径为 `\sqrt3`。

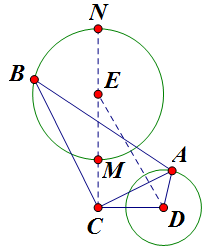
但是，题目限制了 B、D 在 AC 的两侧，易知当 A、C、D 共线时，B 在 M 或 N 处，所以 B 得在 MN 的左边。

所以当 B 由 M 顺时针移动到 N 的过程中，BD 由 DM 增长到 max 再减少到 DN。

易知
`DM=\sqrt{(3-\sqrt3)^2+3}=\sqrt{15-6\sqrt 3}\approx2.14655`，
`DN=\sqrt{(3+\sqrt3)^2+3}=\sqrt{15+6\sqrt 3}\approx5.03905`，
而 max 就是 BED 共线时，得 `\max=3\sqrt3`。

所以：
当 `BD\in\left(\sqrt{15-6\sqrt 3},\sqrt{15+6\sqrt 3}\right]\cup\bigl\{3\sqrt3\bigr\}` 时三角形唯一；
当 `BD\in\left(\sqrt{15+6\sqrt 3},3\sqrt3\right)` 时三角形唯二。

这样选项 BCD 都属于唯一解的情况，而选项 A 的 2.1 与 `\sqrt{15-6\sqrt 3}\approx2.14655` 只差一点点，可见命题者写选项也不是随便写的，故意写一个很接近的，让你难以目测哪个大，只有去平方计算（允许带计算器除外）。

力工

回复 2# kuing
原来这样看的，高！我直接用两圆看，晕死晕死过去了。