来自 MetHodΩ 的两圆相切的性质

hbghlyj

圆O上四点ABCD,任意两圆如图相切,设内位似中心为I,则I在对角线J和O连线上

hbghlyj

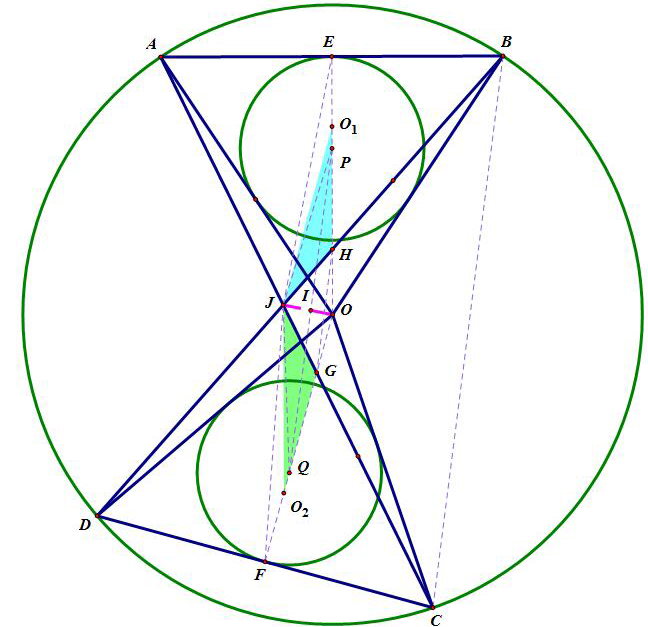
取△ABJ,△CDJ外心$O_1,O_2$.
取AB,CD中点E,F.设OE交BD于点H,OF交AC于点G.
则由$\Delta \mathrm{JHO}_{1} \sim \Delta \mathrm{JGO}_{2} $可知$\frac{\mathrm{JH}}{\mathrm{JG}}=\frac{\mathrm{JO}_{1}}{\mathrm{JO}_{2}}=\frac{\mathrm{BJ}}{\mathrm{CJ}}$
所以$\frac{\mathrm{OJ}}{\mathrm{OB}} \cdot \frac{\sin \angle \mathrm{JOH}}{\sin \angle \mathrm{BOE}}=\frac{\mathrm{JH}}{\mathrm{BH}}=\frac{\mathrm{JG}}{\mathrm{CG}}=\frac{\mathrm{OJ}}{\mathrm{OC}} \cdot \frac{\sin \angle \mathrm{JOF}}{\sin \angle \mathrm{COF}}$
即$\frac{\sin \angle \mathrm{JOH}}{\sin \angle \mathrm{JOF}}=\frac{\sin \angle \mathrm{BOE}}{\sin \angle \mathrm{COF}}$.
故$\frac{[\mathrm{JOE}]}{[\mathrm{JOF}]}=\frac{\mathrm{OEsin} \angle \mathrm{JOH}}{\mathrm{OFsin} \angle \mathrm{JOF}}=\frac{\cos \angle \mathrm{BOE}}{\cos \angle \mathrm{COF}} \cdot \frac{\sin \angle \mathrm{BOE}}{\sin \angle \mathrm{COF}}$
于是$\frac{[\mathrm{JOP}]}{[\mathrm{JOQ}]}=\frac{\mathrm{OP[JOE}]}{\mathrm{OE}} \cdot \frac{\mathrm{OF}}{\mathrm{OQ[JOF}]}=\frac{\cos \angle \mathrm{BOE}}{\mathrm{OE}} \cdot \frac{\mathrm{OF}}{\cos \angle \mathrm{COF}} \cdot \frac{\sin \angle \mathrm{BOE} \cdot \mathrm{OP}}{\sin \angle \mathrm{COF} \cdot \mathrm{OQ}}=\frac{\mathrm{OC}}{\mathrm{OB}} \cdot \frac{\mathrm{PE}}{\mathrm{FQ}}=\frac{\mathrm{PE}}{\mathrm{FQ}}$
$\Rightarrow JIO$共线.