四边形中，等角等边证相等

乌贼

如图：
凸四边形$ ABCD $中$ \angle ABD=\angle ADE,\angle BDC=\angle CBF $,若$ AD=AF $。求证：$ CB=CE $

乌贼

链接：forum.php?mod=viewthread&tid=8082&ext … er=type&typeid=2
这题解，链接中的题也解。

kuing

记 `AE=x`, `EB=y`, `CF=a`, `FD=b`，依题意有 `AD=\sqrt{x(x+y)}`, `BC=\sqrt{a(a+b)}`，如下图所示：

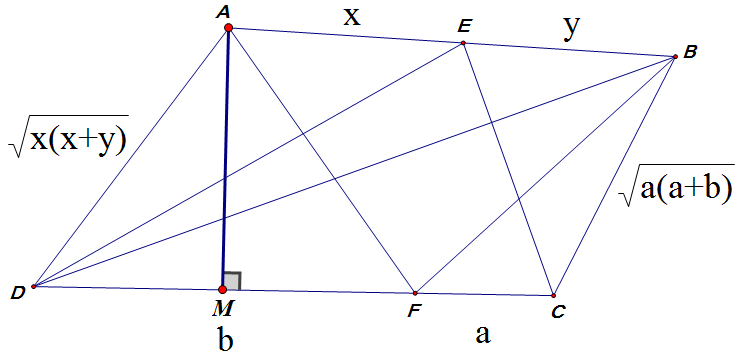
作 `AM\perp CD` 于 `M`，依题意有 `M` 为 `DF` 中点，由勾股定理有
\[AC^2=MC^2+AM^2=\left( a+\frac b2 \right)^2+x(x+y)-\left( \frac b2 \right)^2=a(a+b)+x(x+y),\]于是由余弦定理有
\[\cos\angle ABC=\frac{a(a+b)+(x+y)^2-AC^2}{2\sqrt{a(a+b)}(x+y)}=\frac y{2\sqrt{a(a+b)}},\]也就是
\[BC\cos\angle ABC=\frac y2,\]这就说明了 `CB=CE`。

乌贼

回复 3# kuing
这证法直接暴力

kuing

回复 4# 乌贼

这都算暴力咩？计算量很小喔……