较综合的求三棱锥中的面积和最大值

isee

已知三棱锥$P-ABC$的顶点$P$在底面的射影$O$为$\triangle ABC$的垂心，
若$S_{\triangle ABC}\cdot S_{\triangle OBC}
=S^2_{\triangle PBC}$且三棱锥$P－ABC$的外接球半径为$4$，
则$S_{\triangle PAB}+S_{\triangle PBC}+S_{\triangle PCA}$的最大值为_32_.

乌贼

点$ ABCPF $在球面上，$ \angle APF=90\du ,AF=8 $，也不好弄，猜想$ \triangle ABC $为正三角形时取得……

kuing

借用楼上的图，擦掉 F：

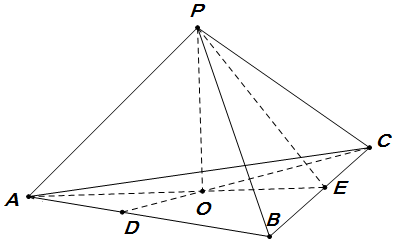
由 `AE\perp BC`, `PO\perp BC` 知 `BC\perp\text{面}~APE`，故 `PE\perp BC`，因此
\[\S{ABC}\cdot\S{OBC}=\S{PBC}^2\iff EA\cdot EO=EP^2\iff AP\perp PE,\]于是
\[AP\perp\text{面}~PBC,\]不仅如此，由 `O` 为垂心得
\[OC\cdot OD=OA\cdot OE=OP^2\iff PC\perp PD,\]因此同样可以推出 `CP\perp\text{面}~PAB` 以及 `BP\perp\text{面}~PAC`，所以实际上这是一个直角四面体。
于是就变成 `a^2+b^2+c^2=8^2` 求 `0.5(ab+bc+ca)` 的最大值，地球人都会。

isee

回复 2# 乌贼


没想到啊，竟然把你卡了一下~

乌贼

回复 4# isee
卡两下，直角四面体一下，$ BC=AF $一下

乌贼

$ a^2+b^2+c^2=(2r)^2 $原来是这样出来的，球内接直角四面体，沿着平面$ PBC $看就有\[AQ^2=PA^2+PQ^2=PA^2+PB^2+PC^2 \]四面体中$ BC $的长度为球上$ PQ $截面圆的直径即$ PQ $

kuing

回复 6# 乌贼

直角四面体直接补回长方体啊，外接球直径就是长方体体对角线啊……