几何证明题。证明几个比值都等于两圆半径之比的平方

TSC999

两圆 S、T  相交于 A、B， AD、AC 是两圆的切线， CB、DB 的延长线交两圆于 E、F，ES、FT 的延长线交 AD、AC 于 M、N，
MN 与 AB 交于 Q， AB 的延长线与 DC 交于 P。证明 :
①  MN 平行于 DC。
②  BP 是 ∠DBC 的平分线。
③ MQ: QN = DB : BC = DP: PC = (RS/RT)^2。其中 RS 和 RT 分别是两圆的半径。

kuing

由弦切角定理，有 $\angle BAC=\angle BDA$ 以及 $\angle BAD=\angle BCA$，得到 $\triangle ABC\sim\triangle DBA$，故 $\angle ABC=\angle ABD$，即得 ②；

以 $m(XY)$ 表示弧 $XY$ 所对圆心角的度数，由 $\angle DBE=\angle CBF$ 得 $m(DE)=m(CF)$，由刚才所证知 $m(AD)=m(AC)$，可见下图的蓝色线与绿色线是整体相似的，所以 $AM:MD=AN:NC$，即得 ①；

由 ① 得 $MQ:QN=DP:PC$，由 ② 及角平分线定理得 $DP:PC=DB:BC$，又由 ② 知 $DB:BC=\S{DAB}:\S{CAB}$，而这俩三角形相似，故面积比 = 相似比的平方 = 外接圆半径之比的平方。

综上所述，命题得证。

乌贼

如图：
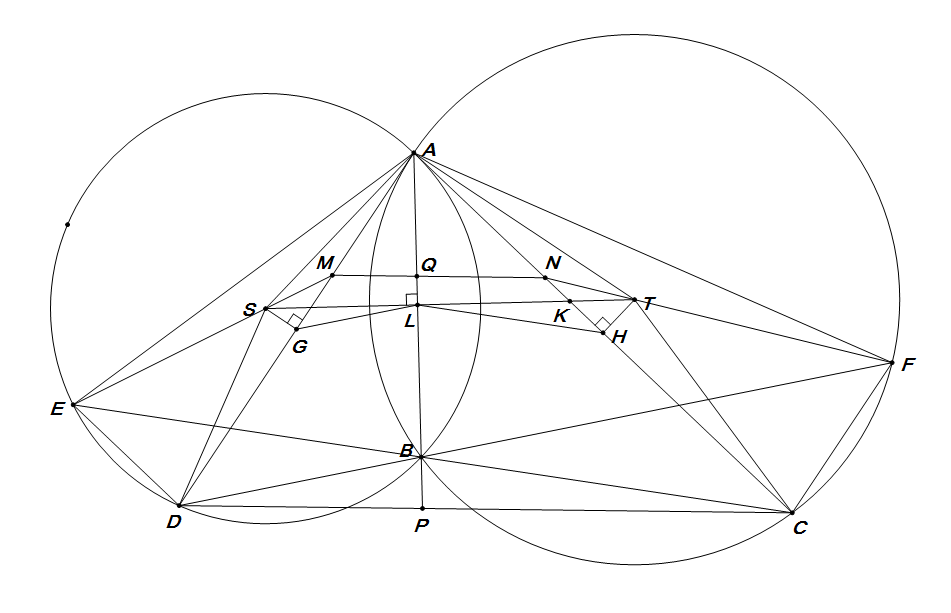
（1）\[ \edr \angle EAD=\angle CAF \\\angle SAD=\angle TAC \endedr\riff\edr\begin{cases}
\triangle EAM\sim \triangle FAN\\\triangle DSA\sim \triangle CTA
\\\triangle ESA\sim \triangle FTA\end{cases}\endedr\riff\dfrac{AM}{AN}=\dfrac{AS}{AT}=\dfrac{AD}{AC}\riff MN\px DC \]
（2）$ G,H $分别为$ AD,AC $的中点，$ L $为$ AB $与$ ST $的交点。有$ ASGL $四点共圆，$ ATHL $四点共圆。\[ \angle SLG=\angle SAG=\angle TAH=\angle TLH\riff\angle DBP=\angle DLB=\angle CLB=\angle CBP \]（3）由\[ \triangle GLS\sim \triangle KHL\riff \dfrac{GL}{SL}=\dfrac{LK}{LH}\riff\dfrac{GL}{LH}=\dfrac{SL\cdot LK}{LH^2}=\dfrac{AL^2}{LH^2} \]又\[ \edr\triangle HLA\sim \triangle TAS\\\dfrac{DB}{DC}=\dfrac{DL}{LH} \endedr\riff\dfrac{DB}{DC}=\dfrac{AL^2}{LH^2}=\dfrac{AS^2}{AT^2}\]

TSC999

回复 2# kuing

蓝线、绿线整体相似，这个论断妙。由此可知若 W 是 AB 或其延长线上的任一点，均有 DW: CW=DB: CB。

kuing

由此可知若 W 是 AB 或其延长线上的任一点，均有 DW: CW=DB: CB。
TSC999 发表于 2021-10-3 17:36

这个并不对喔

TSC999

这个并不对喔
kuing 发表于 2021-10-3 18:09

你说的对，因为不能保持 ∠DWB=∠CWB。

TSC999

由弦切角定理，有 $\angle BAC=\angle BDA$ 以及 $\angle BAD=\angle BCA$，得到 $\triangle ABC\sim\trian ...
kuing 发表于 2021-10-3 01:20

蓝线、绿线整体相似，相似比是多少？ 是不是等于 DB: BC ？ 为嘛这个相似比不等于 ES: TF，而是等于它的平方？

kuing

蓝线、绿线整体相似，相似比是多少？ 是不是等于 DB: BC ？ 为嘛这个相似比不等于 ES: TF，而是等于它的平 ...
TSC999 发表于 2021-10-4 10:45

相似比 = 半径比，也等于 AD : AC，但不等于 DB : BC。
注意 △DBA ∽ △ABC 的字母顺序，DB 与 BC 并不是对应边。

这的确很容易搞错。
蓝线与绿线整体相似，同时 △DBA ∽ △ABC，很容易误以为“蓝线 + △DBA”与“绿线 + △ABC”形成了一个更大的整体相似，但其实不是。

实际上由 △DBA ∽ △ABC 得 DA : AC = DB : AB = BA : BC ，由此可得 $(DA : AC)^2 = (DB : AB)\times(BA : BC) = DB : BC$，所以其实 2# 最后一步也可以不用面积来证。

TSC999

回复 8# kuing
谢谢 Kuing 大神的解释！ 水平确实高！