江苏卷 二试P1

大佬最帅

江苏卷 二试P1是否可以提出一个推广

乌贼

如图：
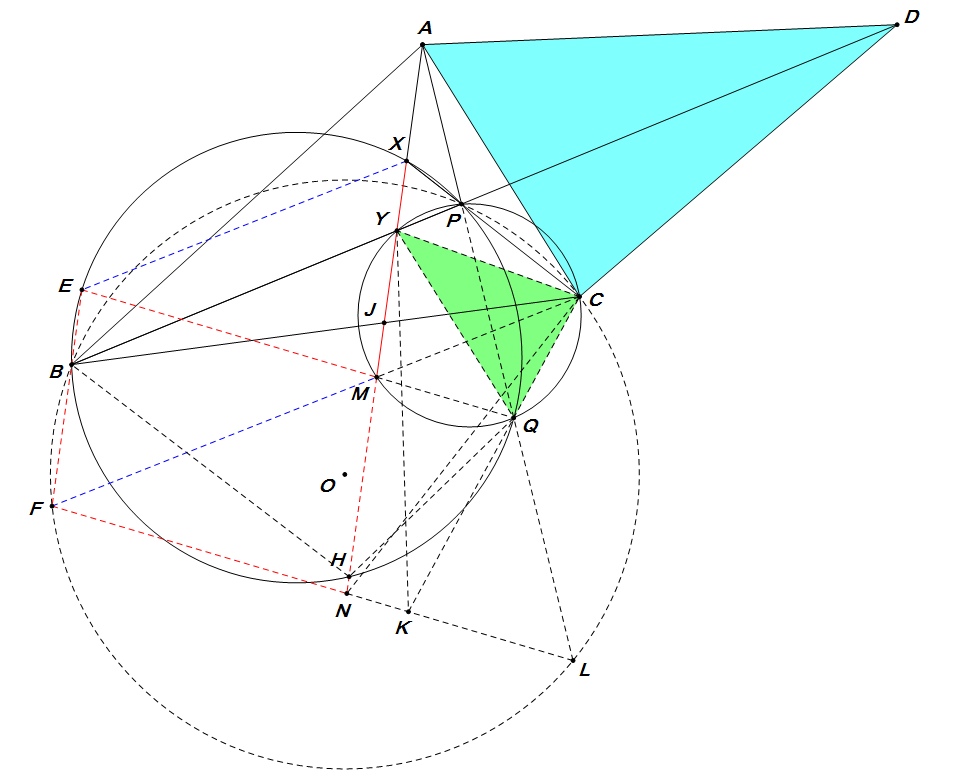
    延长$ BP $至$ D $，使$ AD=AB $。有$ ADCP $四点共圆，得\[ \angle CAD=\angle CPD=\angle XPY=\angle CQY \]
作$ \triangle BCP $外接圆$ O $，延长$ AY $分别交$ BC $交圆$ W_2,W_1 $于$ J,M,H $，延长$ QM $交圆$ W_1 $于$ E $。易证$ \triangle BHY\sim \triangle XPY\sim \triangle XMC,\angle BHY=\angle XPY=\angle XMC,HB=HY,PX=PY,MX=MC $。
又
\[ \edr \angle QYC=\angle QPC=\angle QHM \\\angle QCY=\angle QMH \endedr\riff\angle MQH=\angle CQY=\angle XPY\riff EH=BX\riff BE\px XH\riff\angle EXH=\angle BHX=\angle XMC\riff EX\px MC \]延长$ CM $交圆$ O $于$ F $，有\[ \angle BFC=\angle XPY=\angle XMC\riff BF\px XH \]且$ EBF $三点共线，$ EFMX $为平行四边形，得\[ EF=MX=MC \]
再延长$ PQ $交圆$ O $于$ L $，连接$ FL $，$ N，K $分别为$ FL $与$ AH $（或其延长线），$ CQ $延长线交点。有\[ \angle PLF+\angle PBF=\angle PLF+\angle PYM=180\du =\angle PQM+\angle PYM\riff\angle PLF=\angle PQM\riff EQ\px FL  \]即$ EFNM $为平行四边形，且$ CKNY $四点共圆。所以\[ MN=EF=MX=MC \]\[ \angle MCN=\angle MNC=\dfrac{1}{2}\angle YMC\riff\angle YKQ=\angle MNC=\dfrac{1}{2}\angle YMC=\dfrac{1}{2}\angle YQC=\angle KYQ\riff QK=QY \]
因此\[ \edr\dfrac{CQ}{QY}=\dfrac{CQ}{QK}=\dfrac{CM}{MF}=\dfrac{CJ}{JB}=\dfrac{AC}{AB}=\dfrac{CA}{AD}\\\angle CAD=\angle CQY\endedr\riff\triangle CAD\sim \triangle CQY \]故\[ \angle CPQ=\angle CYQ=\angle CDA=\angle APX \]也就是$ APQ $三点共线
唉，初等几何折磨人，用根轴……见forum.php?mod=viewthread&tid=8250&extra=#pid41390 5楼，9楼

乌贼

tieba.baidu.com/p/7565503673