解方程 `x^6+4x^3-6x+2=0`

kuing

86鱼 2021/11/29 21:25:59

kuing 2021/11/29 21:26:37

记 `x^3=2` 的三个根为 `a`, `b`, `c`，则
\[x^6+4x^3-6x+2=(x^2-ax+a^2-a)(x^2-bx+b^2-b)(x^2-cx+c^2-c),\]所以，记 `\omega=\cos120\du+\sin120\du\cdot i`，则六个根为
\[x=\frac{\sqrt[3]2\pm\sqrt{4\sqrt[3]2-3\sqrt[3]4}}2,\,\frac{\sqrt[3]2\omega\pm\sqrt{4\sqrt[3]2\omega-3\sqrt[3]4\omega^2}}2,\,\frac{\sqrt[3]2\omega^2\pm\sqrt{4\sqrt[3]2\omega^2-3\sqrt[3]4\omega}}2.\]
要是不提示那一个根，根本看不出可以解

真神奇……

isee

神, 奇

kuing

话说，反过来想，按这种方法，这样的题目可以随便构造。
比如将 2 改成 3，即设 `x^3=3` 的三根 `a`, `b`, `c`，右边的连乘式随便改改系数，比如
`(x^2 - a x + 2 a^2 - 3 a) (x^2 - b x + 2 b^2 - 3 b) (x^2 - c x + 2 c^2 - 3 c)`，
展开时利用 `a+b+c=ab+bc+ca=0`, `abc=3` 得出结果为 `x^6 + 15 x^3 + 27 x^2 - 81 x - 9`，
于是得到题目：
解方程 `x^6 + 15 x^3 + 27 x^2 - 81 x - 9 = 0`，已知一根为 `x=\frac12\left(\sqrt[3]3+\sqrt{12\sqrt[3]3-7\sqrt[3]9}\right)`。
当然这不够 1# 的好看，但原理就是酱紫了

kuing

顺便把这个也贴在这儿：

86鱼 2021/11/14 20:03:02

kuing 2021/11/14 20:03:18

1）`x^5+x+1=0`
注意到三次单位复根满足，所以有因式 `1 + x + x^2`，下略；

2）`x^5-5x^3+5x-4=0`
令 `x = t + 1/t` 展开为 `t^{10} - 4 t^5 + 1 = 0`，下略；

6）`x^6 - 2 x^5 - 7 x^4 + 6 x^3 + 18 x^2 + 8 x + 1 = (x^3-x^2-4x-1)^2`，下略；

7）`x^6 + 4 x^5 - 5 x^4 - 13 x^3 + 4 x^2 + 9 x + 1 = 0`
配方为 `(x^3+2x^2+6x+5/2)^2=21(x^2+x+1/2)^2`，下略。

isee

回复 3# kuing


这么一说，有点像利用利用单位根因式分解，如 $$x^5+x^4+x^2+x+2,$$又三次单位根 $\omega$ 是其一根，因为 $\omega^5+\omega^4+\omega^2+\omega+2=\omega^2+\omega+\omega^2+\omega+2=2(\omega^2+\omega+1)=0$，于是复数范围内 $$x^5+x^4+x^2+x+2=(x-\omega)(x-\bar{\omega})g(x),$$
而 $$(x-\omega)(x-\bar{\omega})=(x-\omega)(x-\omega^2)=x^2+x+1,$$于是 $$g(x)=x^3-x+2,$$
即有 $$x^5+x^4+x^2+x+2=(x^2+x+1)(x^3-x+2).$$

isee

回复 4# kuing

哈哈哈，看刚开始都是 5 次，（1）与楼上不谋而合~~~

isee

顺便把这个也贴在这儿：

1）`x^5+x+1=0`
注意到三次单位复根满足，所以有因式 `1 + x + x^2`，下略；

2） ...
kuing 发表于 2021-12-1 14:12

擦，瞬间你都解了

kuing

回复 7# isee

还有 3 4 5 未解

kuing

3）`x^5+30x^2+15x+2=0`
配为
\[(5x^2-1)^2=(-4x-7)(x^2-4x-1)^2,\]在 `\Bbb R` 内解，需 `x<-7/4`，此各括号内均正，开荒即
\[5x^2-1=\sqrt{-4x-7}(x^2-4x-1),\]令 `\sqrt{-4x-7}=2m+1`，即 `x=-m^2-m-2`，代入就变成
\[m^5+5m^3+5m-4=0,\]和第二题仅差一符号，于是类似地令 `m=t-1/t`，变成 `t^{10}-4t^5-1=0`，下略。

isee

回复 10# kuing

可以命名求个虚根，先

hbghlyj

there are only five solvable quintic equations of the form $x^5+ax^2+b=0,~~a,b \in \mathbb{Q}$:$$x^5-2s^3x^2-\frac{s^5}{5}=0 $$
$$ x^5-100s^3x^2-1000s^5=0 $$
$$x^5-5s^3x^2-3s^5=0  $$
$$x^5-5s^3x^2+15s^5=0  $$
$$ x^5-25s^3x^2-300s^5=0 $$

kuing

4）`x^5 - 11 x^3 - 11 x^2 + 11 x + 11 = 0`
用 WATSON'S METHOD OF SOLVING A QUINTIC EQUATION 里的方法，最终算出根为
\begin{align*}
x={}&\omega\left(\frac{11}{1250}\left(-175-80 \sqrt{5}+i \sqrt{3925+1282 \sqrt{5}}\right)\right)^{1/5}\\
&+\omega^2\left(\frac{11}{1250}\left(-175+80 \sqrt{5}+i \sqrt{3925-1282 \sqrt{5}}\right)\right)^{1/5}\\
&+\omega^3\left(\frac{11}{1250}\left(-175+80 \sqrt{5}-i \sqrt{3925-1282 \sqrt{5}}\right)\right)^{1/5}\\
&+\omega^4\left(\frac{11}{1250}\left(-175-80 \sqrt{5}-i \sqrt{3925+1282 \sqrt{5}}\right)\right)^{1/5},
\end{align*}其中 `\omega` 为任意五次单位根，即 `\omega=\cos(2k\pi/5)+i\sin(2k\pi/5),k=1,2,3,4,5`。

这个是真坑……

kuing

又来了：

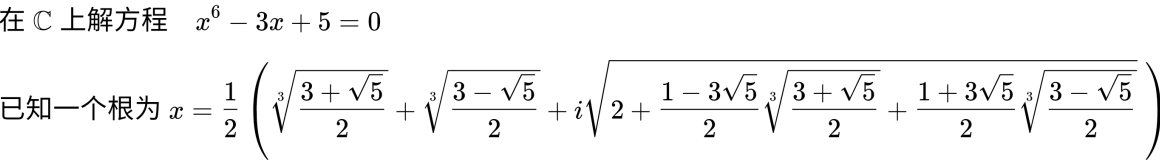
还是 1#、3# 那种套路喔：

设 `a`, `b`, `c` 是 `x^3 + 3 x - 1 = 0` 的三根，即 `a + b + c = 0`, `a b + b c + c a = 3`, `a b c = 1`，则
\[
\bigl(x^2 - (a^2 + 2) x + a + 1\bigr) \bigl(x^2 - (b^2 + 2) x + b + 1\bigr) \bigl(x^2 - (c^2 + 2) x + c + 1\bigr)
= x^6 - 3 x + 5,
\]`a`, `b`, `c` 的具体值为 `-\omega\sqrt[3]{\frac{\sqrt{5}-1}{2}}+\omega^2\sqrt[3]{\frac{\sqrt{5}+1}{2}}`，其中 `\omega` 为任意三次单位根。

kuing

没完没了86鱼

设 `a_1`, `a_2`, `a_3`, `a_4` 是 `x^4+4x+2=0` 的四根，则
\[
\prod_{i=1}^4(x^2+a_ix-a_i^3+a_i^2-a_i-3)=x^8-8x^3-12x^2-1,
\]又设 `b` 满足 `4b^3-2b-1=0`，则
\[
\left( x^2+2\sqrt bx+2b-\frac1{\sqrt b} \right)
\left( x^2-2\sqrt bx+2b+\frac1{\sqrt b} \right)
=x^4+4x+\frac{4b^3-1}b=x^4+4x+2.
\]