如何算出 E、F 点的复数坐标？条件见图。

TSC999

TSC999

问题来源见下图。此图为史勇先生所创。据说他是按 “复对合” 理论算出的 E、F 点的复坐标。

TSC999

TSC999

求 E 点坐标的程序代码：

1. Clear["Global`*"];
2. h = a^2 + b^2 + c^2;  
3. \!\(\*OverscriptBox[\(h\), \(_\)]\) = 1/a^2 + 1/b^2 + 1/c^2;
4. Timing[Simplify[
5.   Solve[{Sqrt[(a^2 - b^2) (1/a^2 - 1/b^2)] Sqrt[(b^2 - e) (1/b^2 -
6. \!\(\*OverscriptBox[\(e\), \(_\)]\))] == (a^2 - c^2) (1/a^2 -
7.          1/c^2) - (b^2 - c^2) (1/b^2 - 1/c^2), (h - b^2)/(
8. \!\(\*OverscriptBox[\(h\), \(_\)]\) - 1/b^2) == (e - b^2)/(
9. \!\(\*OverscriptBox[\(e\), \(_\)]\) - 1/b^2)}, {e}, {
10. \!\(\*OverscriptBox[\(e\), \(_\)]\)}]]]

Copy the Code

求 F 点坐标的程序代码：

1. Clear["Global`*"];
2. h = a^2 + b^2 + c^2;  
3. \!\(\*OverscriptBox[\(h\), \(_\)]\) = 1/a^2 + 1/b^2 + 1/c^2;
4. Timing[Simplify[
5.   Solve[{Sqrt[(a^2 - c^2) (1/a^2 - 1/c^2)] Sqrt[(c^2 - f) (1/c^2 -
6. \!\(\*OverscriptBox[\(f\), \(_\)]\))] == (a^2 - b^2) (1/a^2 -
7.          1/b^2) - (b^2 - c^2) (1/b^2 - 1/c^2), (h - c^2)/(
8. \!\(\*OverscriptBox[\(h\), \(_\)]\) - 1/c^2) == (f - c^2)/(
9. \!\(\*OverscriptBox[\(f\), \(_\)]\) - 1/c^2)}, {f}, {
10. \!\(\*OverscriptBox[\(f\), \(_\)]\)}]]]

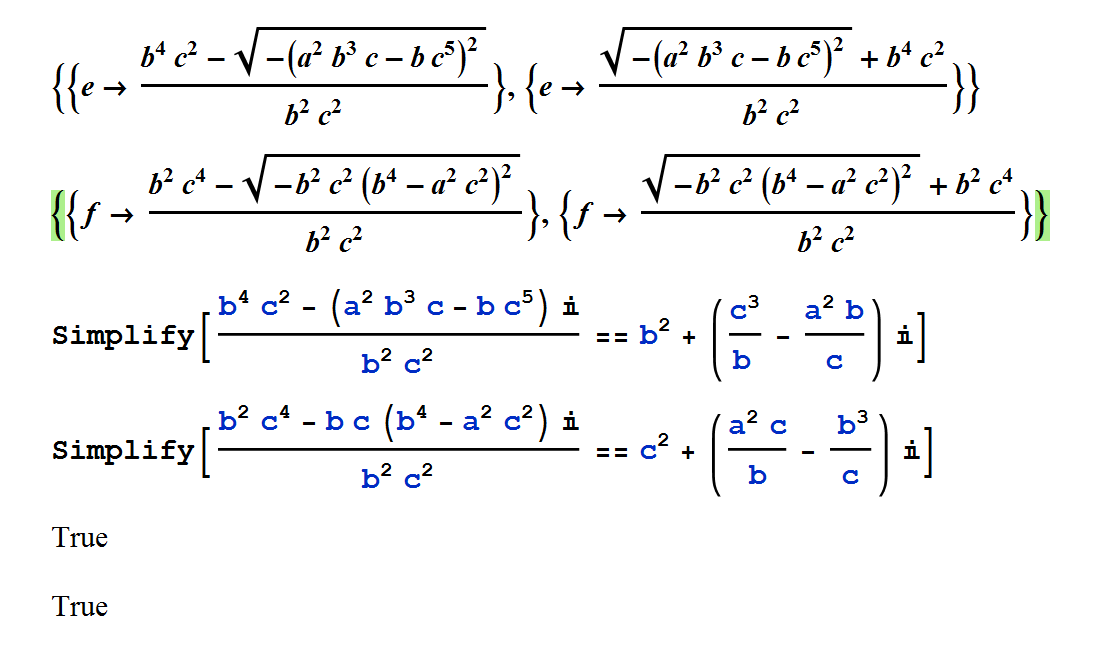
Copy the Code

上面程序解出的 E、F 是未化简坐标，消除根式后正负号如何取？ 可通过数字验证来判断。根式消除后，下一步可用软件来证明主帖中的史勇公式：