求助

xcx

如图, 以 $A$ 为圆心作一个圆 $\omega$ 与圆 $(A B C)$ 交于 $D, E$ 两点. $D E$ 与边 $A B, A C$ 分别交于 $F, G .$ 线段 $B G, C F$ 与圆 $\omega$ 交于点 $J, K$, 圆 $(A B K)$ 与 $(A C J)$ 交于另外一点 $L$. 证明:
$A L, B G, C F$ 三线共点.

战巡

回复 1# xcx

这里首先解决另一个问题

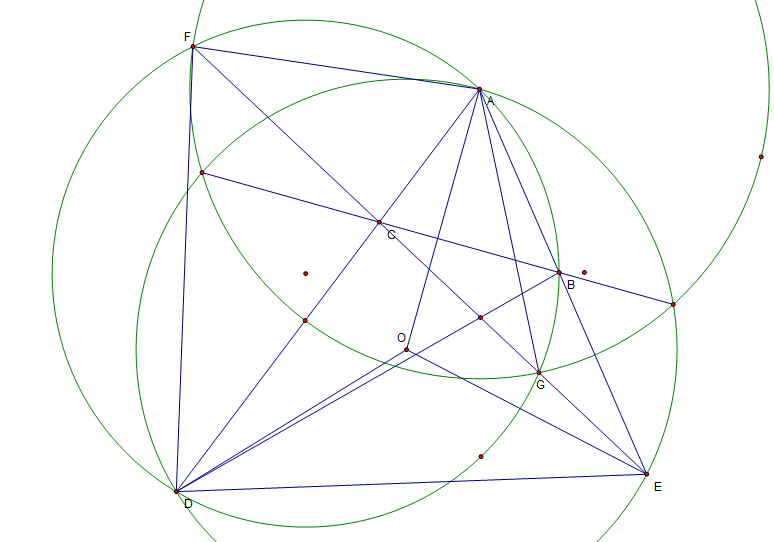
如图，三角形$ADE$中，圆$A$与$\Delta ADE$外接圆的公共弦与$AD,AE$分别交于$C,D$，作$\Delta ABD$外接圆，其与$\Delta ADE$外接圆公共弦为$FG$，证明$F,C,G,E$共线

首先，我们假设$\Delta ADE$外接圆方程为$C_1(x,y)=0$，具体是啥不重要，同理令圆$A$方程为$C_2(x,y)=0$，和$\Delta ADE$外接圆方程为$C_3(x,y)=0$

如此我们知道这些公共弦的方程，有
\[BC:C_1(x,y)-C_2(x,y)=0\]
\[FG:C_3(x,y)-C_2(x,y)=0\]
注意$AD$其实就是$C_1$和$C_3$的公共弦，因此有
\[AD:C_1(x,y)-C_3(x,y)=0\]
考虑到$C$点正是上面两条线的交点，因此有
\[\begin{cases}C_1(x_C,y_C)-C_2(x_C,y_C)=0\\C_1(x_C,y_C)-C_3(x_C,y_C)=0\end{cases}\]
这两条相减，就得到
\[C_3(x_C,y_C)-C_2(x_C,y_C)=0\]
也就是说，$C$点正在$FG$上，因此$C,F,G$共线
这个结论如果更抽象概括一点，就是这样的：如果三个圆两两相交，则三条公共弦会交于一点

接下来连$EC$、$AF$、$DF$，令$ADE$外接圆圆心为$O$，连$OA,OD,OE$
如此很显然会有$AO\perp BC$，而且令$\angle OAD=\angle ODA=X,\angle OAE=\angle OEA=Y,\angle ODE=\angle OED=Z$
然后有
\[\begin{cases}X+Y=\angle A\\ X+Z=\angle D\\ Y+Z=\angle E\end{cases}\]
很容易得到
\[X=\frac{1}{2}(\angle A+\angle D-\angle E)=90\du-\angle E\]
继而有$\angle ACB=\angle AED$，同理$\angle ABC=\angle ADE$，这个可以证明$\Delta ABC\sim \Delta ADE$，然后$\frac{AB}{AD}=\frac{AC}{AE}$，然后$\Delta ABD\sim\Delta ACE$，$\angle ACE=\angle ABD$

另一方面，$F,G$都在圆$A$上，显然有$AF=AG$，这使得$\angle AFG=\angle AGF=\angle ADF$，于是$\angle FCA=\angle DFA=180\du-\angle ABD$，这就说明$\angle FCA+\angle ACE=180\du$，继而$F,C,G,E$共线



证明完这个以后，重新来看这道题，你就会发现，按照上面的结论，会有$A,F,C,J$共圆和$A,G,K,B$共圆
然后按照上面那题中证明$C,F,G$共线的套路，就很容易证明这里$AL,FK,JG$共点

mowxqq

用根心定理套一下就可以吧
令四个圆为 $O_1、O_2、O_3、O_4$，
则 $O_1、O_2、O_4$ 的根轴 $PK、AB、DE$ 共点 $F$，即 $P、F、K、C$ 共线；
$O_1、O_3、O_4$ 的根轴 $JQ、AC、DE$ 共点 $G$，即 $Q、G、J、B$ 共线，
故 $O_1、O_2、O_3$ 的根轴 $FK、JG、AL$ 也共点

xcx

感谢 发完就想起来根心 忘删帖了