侧面积最小 四面体

hbghlyj

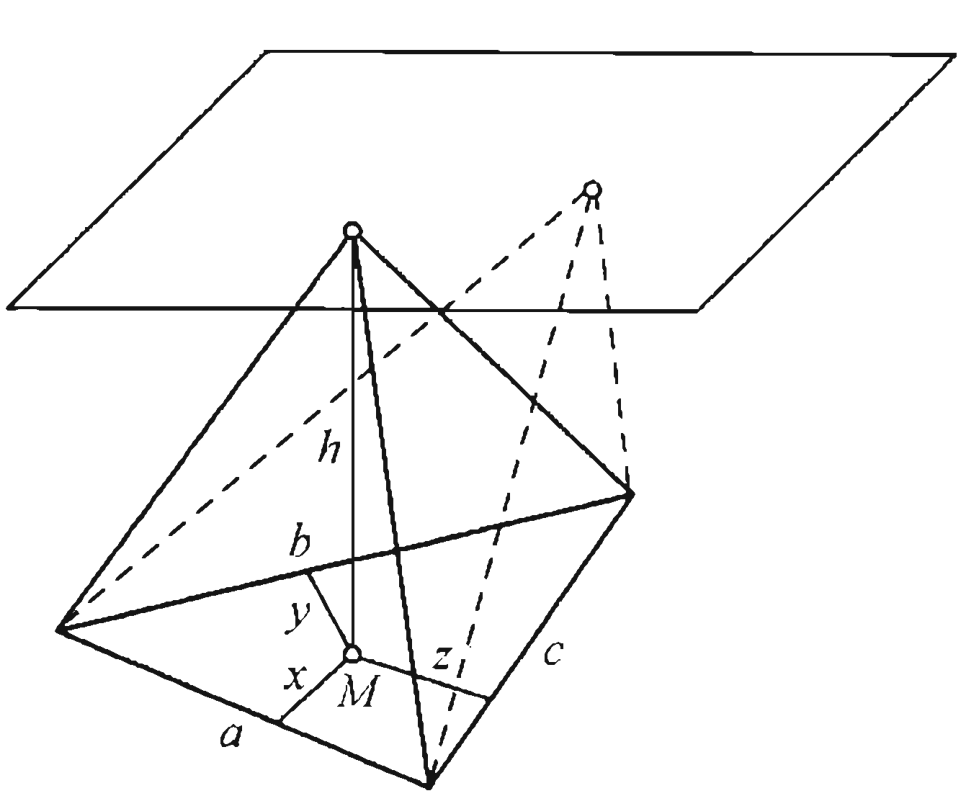
在平面上给定一个边长为$a,b,c$的三角形;在它上面可作无数个有已知高$h$的锥体.要在其中求出有最小侧面积$S$的那一个.
问题变成要去求锥体顶点的投影$M$,它的位置由边$a,b,c$上的三条垂线$x,y,z$的数量所确定.若这点与三角形本身位于边的同侧,则垂线之前附以正号,否则附以负号.数量$x,y,z$由下列关系式联系着($P$表示三角形的面积):$$a x+b y+c z=2 P$$
侧面积$S$就可表示为:$$S=\frac{a}{2} \sqrt{x^{2}+h^{2}}+\frac{b}{2} \sqrt{y^{2}+h^{2}}+\frac{c}{2} \sqrt{z^{2}+h^{2}}$$令$r=\frac{2P}{a+b+c}$(内切圆半径).
由柯西不等式,$(r^2+h^2)(x^2+h^2)\ge(rx+h^2)^2$
所以$\sqrt{x^2+h^2}\ge\frac{rx+h^2}{\sqrt{r^2+h^2}}$
所以$S\ge\frac{r(ax+by+cz)+h^2(a+b+c)}{2\sqrt{r^2+h^2}}=\frac{2Pr+h^2(a+b+c)}{2\sqrt{r^2+h^2}}$
当$x=y=z=r$时取等.