如图 一个三角形面积公式求证明或者证伪

xhz76B

xhz76B

求解答........

kuing

记 `BC=a` 等，内切圆半径为 `r`，则 `2S=r(a+b+c)`，于是要证的等式等价于
\[(r+AD)a+(r-BF)b+(r-CE)c=0,\]
过内心 `I` 作切线的平行线 `l` 与 `AD`, `BF`, `CE` 分别交于 `D'`, `F'`, `E'`，则上式变为
\[AD'\cdot a+(-BF')\cdot b+(-CE')\cdot c=0,\]
建坐标系，使 `x` 轴平行于 `l`，如下图。

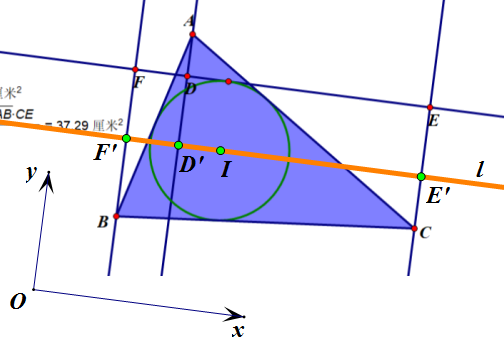
设 `A(x_1,y_1)`, `B(x_2,y_2)`, `C(x_3,y_3)`，则 `I` 的坐标为
\[I\left( \frac{ax_1+bx_2+cx_3}{a+b+c},\frac{ay_1+by_2+cy_3}{a+b+c} \right),\]
记 `I` 的纵坐标为 `y_I`，则
\begin{align*}
&AD'\cdot a+(-BF')\cdot b+(-CE')\cdot c\\
={}&(y_1-y_I)a+(y_2-y_I)b+(y_3-y_I)c\\
={}&\frac{b(y_1-y_2)+c(y_1-y_3)}{a+b+c}\cdot a\\
&+\frac{a(y_2-y_1)+c(y_2-y_3)}{a+b+c}\cdot b\\
&+\frac{a(y_3-y_1)+b(y_3-y_2)}{a+b+c}\cdot c,
\end{align*}
化简后显然为 `0`，即得证。

isee

回复 3# kuing


也就你能写顺手，哈哈哈

爪机专用

回复 4# isee

你来一个纯几何法呗

hbghlyj

将$$\overrightarrow0=BC·\overrightarrow{AI}+CA·\overrightarrow{BI}+AB·\overrightarrow{CI}$$
投影到AD方向得$$0=BC·(-AD-r)+CA·(BF-r)+AB·(CE-r)$$
除以2得$$0=\frac{BC·(-AD-r)+CA·(BF-r)+AB·(CE-r)}2$$
与$$\S{ABC}=\frac{BC·r+CA·r+AB·r}2$$相加得$$\S{ABC}=\frac{-BC·AD+CA·BF+AB·CE}2$$

kuing

回复 6# hbghlyj

圆奶乳齿呀，我竟然还建系

isee

回复 6# hbghlyj


哈哈哈，我把4＃后半句＂看着像向量＂给删了，主要怕追问，不曾想还真的行

kuing

回复 8# isee

所以有想法就应该上