|
|
在圆内接四边形ABCD中,一条直线L分别交AB、BC、CD、DA于P、Q、R、S,若圆上四点A'、B'、C'、D'满足A'B'过P、B'C'过Q、C'D'过R,则D'A'过S.
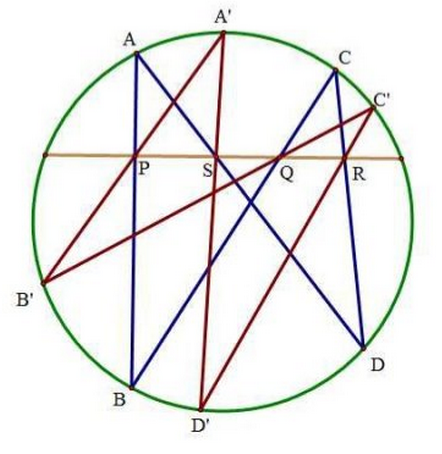
证:设AC'交A'C于T,AD交A'D'于S'.
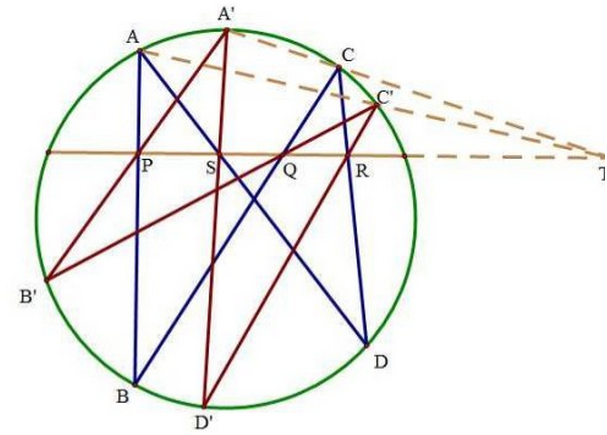
由Pascal定理,在圆内接六边形ABCA'B'C'中,AB交A'B'于P、BC交B'C'于Q、CA'交C'A于T共线,即T在L上.
由Pascal定理,在圆内接六边形ADCA'D'C'中,AD交A'D'于S'、DC交D'C'于R、CA'交C'A于T共线,即S'在L上,故S与S'同一,即D'A'过S.
|
|