$P_1,P_2,P_3,P_4$在一条circular cubic上.$P_1P_2,P_3P_4$交曲线于$P_{12},P_{34}$.
$P_1,P_2,P_3,P_4$共圆,当且仅当$P_{12}P_{34}$经过曲线的渐近线的无穷远点.
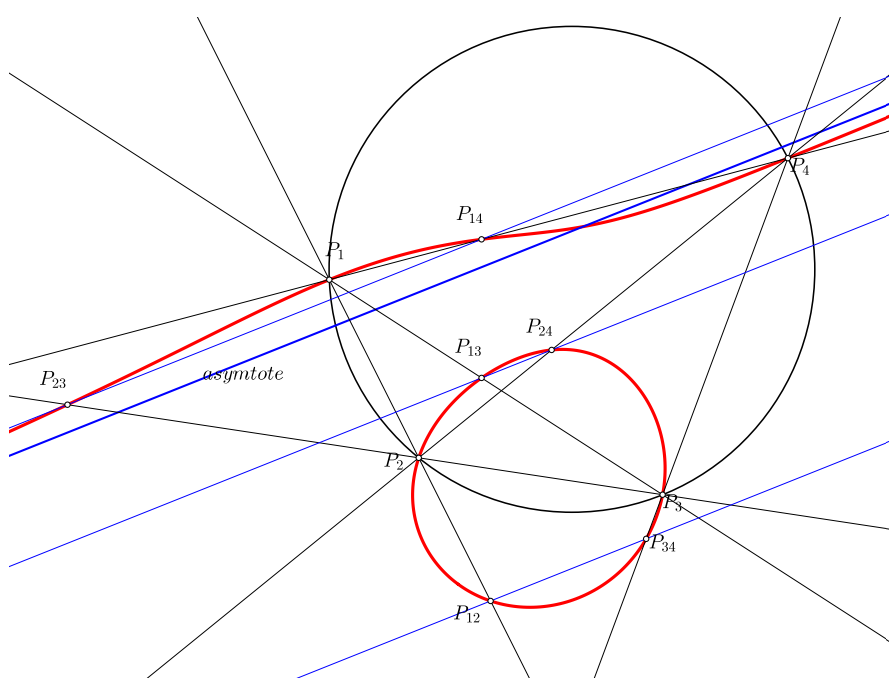
设$W$为渐近线的无穷远点,$J_1,J_2$为圆环点.$P_1,P_2,P_3,P_4$共圆⇔$P_1,P_2,P_3,P_4,J_1,J_2$共锥线.
circular cubic和退化三次曲线$\left(\overline{P_{1}, P_{2}, P_{12}}, \overline{P_{3}, P_{4}, P_{34}}, \overline{J_{1}, J_{2}, W}\right)$有9个交点$P_{1}, P_{2}, P_{3}, P_{4}, P_{12}, P_{34},J_1,J_2,W$.考虑锥线$P_{1} P_{2} P_{3} P_{4} J_{1} J_{2}$与直线$\overline{P_{12} P_{34}}$之并,它是一条退化三次曲线,通过其中8个点,由Cayley - Bacharach 定理,其通过第9点$W$,即$\overline{P_{12}P_{34}}$通过$W$.
反过来,若$\overline{P_{12}P_{34}}$通过$W$,对circular cubic,$\left(\overline{J_{1}, J_{2}, W}, \overline{P_{1}, P_{2}, P_{12}}, \overline{P_{3}, P_{4}, P_{34}}\right),\left(\overline{W, P_{12}, P_{34}}, P_{1} P_{2} P_{3} J_{1} J_{2}\right)$应用Cayley - Bacharach 定理,得$P_{1}, P_{2}, P_{3}, P_{4}, J_{1}, J_{2}$共锥线.
来源 |