|
|
这篇文章
Let given triangle $A B C$ and circle $\omega$ which goes through points $B, C$. Let $M$ be any point outside circle $\omega$. Let $\pi$ be incircle of triangle $A B C$ and let line $l$ be tangent line to $\pi$ which is parallel to line $B C$. Let tangent lines through point $M$ to circle $\pi$ intersect line $l$ at two points $X_{1}, X_{2}$. Consider two circles $\omega_{1}, \omega_{2}$ which are internally tangent to circle $\omega$ and also tangent to lines $A B, A C$. Consider circle $\psi$ which is internally tangent to circle $\omega$ and also is tangent to lines $M X_{1}, M X_{2}$ Then there exists circle $\tau$ which goes through points $X_{1}, X_{2}$ and is tangent to circles $\omega_{1}, \psi$. (Figure 1 )
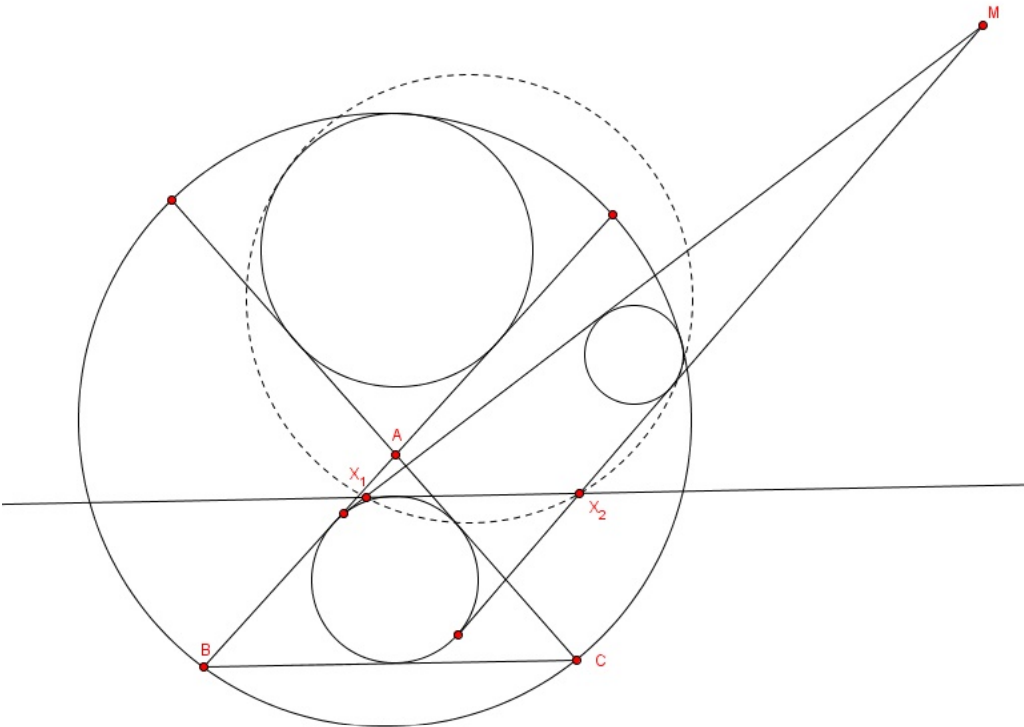
给定$△A B C$和过$B,C$的圆$\omega$.设$M$为$\omega$外的任一点.设$\pi$为$△A B C$的内切圆,$l$与$\pi$相切且平行于$B C$.过$M$作$\pi$的切线交$l$于两点$X_{1}, X_{2}$.作圆$\omega_{1}, \omega_{2}$,它们内切于$\omega$且与$A B, A C$相切.作圆$\psi$,内切于$\omega$且与$M X_{1}, M X_{2}$相切.求证:存在圆$\tau$,经过$X_{1}, X_{2}$且与$\omega_{1}, \psi$相切.
注:未画出$\omega_2$.另外,$\psi$其实也是有两个. |
|