过焦点在渐近线上的投影作实轴平行线

hbghlyj

6056经过djc简化后:
双曲线$Γ$，$O$是中心，过一个焦点$F$作一条渐近线的垂线，垂足为$M$，过$M$作实轴的平行线交$Γ$于$P$，过$P$作$Γ$的切线交实轴于$Q$.
求证：$OQ$=$PQ$

战巡

回复 1# hbghlyj


令$M:(x_M,y_M)$，那么按射影定理，会有
\[y_M^2=x_M\cdot(c-x_M)\]
再加上$M$在$y=\frac{b}{a}$上，可以得到
\[x_M=\frac{a^2}{c},y_M=\frac{ab}{c}\]
然后$y_P=y_M$，故此
\[\frac{x_P^2}{a^2}-\frac{y_P^2}{b^2}=1\]
得到
\[x_P=\frac{a}{c}\sqrt{a^2+c^2}\]
那条切线显然有方程
\[\frac{x_P}{a^2}x-\frac{y_P}{b^2}y=1\]
其与$x$轴交点，当然在
\[x_Q=\frac{a^2}{x_P}=\frac{ac}{\sqrt{a^2+c^2}}\]
那么
\[PQ^2=(x_P-x_Q)^2+y_P^2=\left(\frac{a}{c}\sqrt{a^2+c^2}-\frac{ac}{\sqrt{a^2+c^2}}\right)^2+\frac{a^2b^2}{c^2}\]
\[=\frac{a^6}{c^2(a^2+c^2)}+\frac{a^2(c^2-a^2)}{c^2}=\frac{a^2c^2}{a^2+c^2}=x_Q^2\]

kuing

设渐近线与实轴夹角为 `\theta`，则 `\tan\theta=b/a`，于是 `\cos\theta=a/c`，所以
\[OM=OF_1\cos\theta=c\cos\theta=a,\]
那么点 `M` 的横坐标为
\[x_M=OM\cos\theta=\frac{a^2}c,\]
这说明 `M` 恰好在右准线 `l` 上，于是由第二定义，有
\[\frac{PF_1}{PM}=e=\frac ca=\frac{OF_1}{OM},\]
由此可见 `P`, `O` 两点在以 `F_1`, `M` 为＊＊的某个阿氏圆上，记该圆为 `\omega`，如下图。

由 `OM\perp MF_1` 可知 `OF_1` 与 `\omega` 相切（于 `O`），下面证明：双曲线也与 `\omega` 相切（于 `P`）。

假设双曲线与 `\omega` 有另一交点 `P'`，作 `P'H\perp l` 于 `H`，如下图。

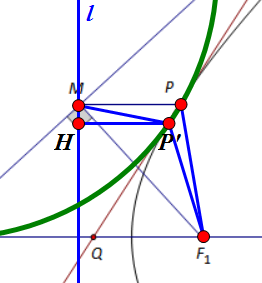
由 `P'` 在阿氏圆上，有 `P'F_1:P'M=PF_1:PM=e`；
由 `P'` 在双曲线上，有 `P'F_1:P'H=e`。
于是 `P'M=P'H`，矛盾！

这样，双曲线在 `P` 处的切线也就是 `\omega` 的切线，而实轴也与 `\omega` 相切，那么由切线长相等就得到 `OQ=PQ`。