|
|
必须记录“坛”
题：若 $AD$ 为锐角 $\triangle ABC$ 的高， $H$ 为 $AD$ 上任一点，直线 $BH$ 交 $AC$ 于点 $E$， $CH$ 交 $AB$ 于点 $F$ . 求证： $\angle EDA=\angle FDA.$
此处加了锐角三角形这个条件，以便 $AD$ 在三角形内，便于叙述，言外之意，高在形外亦成立.
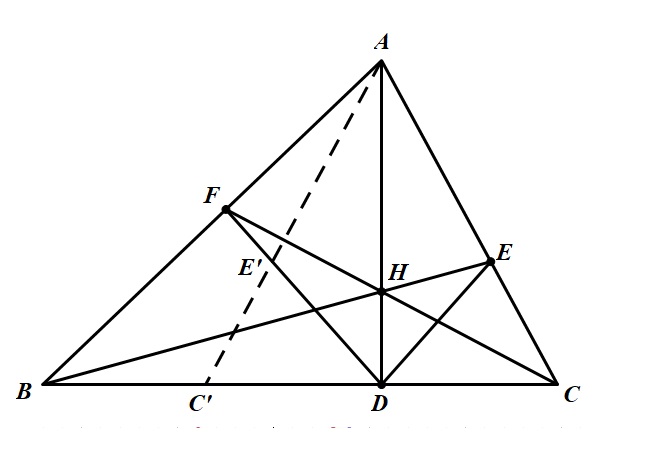
图 1
如图 1，点 $E,{~}C$ 关于直线 $AD$ 的对称点分别为 $C',{~}E'$.
在 $\triangle ABC$ 中由 Ceva 定理有
$\frac {AF}{FB}\cdot \frac {BD}{DC}\cdot \frac {CE}{EA}=1,$ 于是
$\frac {AF}{FB}\cdot \frac {BD}{DC'}\cdot \frac {C'E'}{E'A}=1.$
从而在 $\color{#FE0210}{\triangle ABC'}$ 中由 Menelaus 定理知 $\color{#FE0210}{F,{~}E',{~}D}$ 三点共线，即点 $E'$ 落在直线 $DF$ 上，所以 $\angle EDA=\angle FDA.$ |
|
hbghlyj
Posted 2022-4-11 00:58
