解析几何题的一般情况

力工

已知点$P$关于二次曲线$F$的极线为$l$,过点$P$的直线交$F$于$A,B$，过$A,B$作两平行线交$l$于点$C,D$，若$\triangle APD,\triangle CPD,\triangle  BPC$的面积为$S_1,S_2,S_3$，证明：$S_2^2=4S_1S_3$.

kuing

待证结论打错了吧？
PS、最好配个图

力工

回复 2# kuing
对对对，下标错了，已改并添图了。

kuing

回复 3# 力工

我用几何画板测量过发现并不成立啊，是不是漏了什么条件？
这是你在研究某道题时自己尝试的推广？如果是这样你最好把原题给出来先。

kuing

知道了，原来你的待证结论依然没打对，漏了一个系数 4。
事关我想起了这帖：forum.php?mod=viewthread&tid=7259#pid36438

力工

原题是湖北09年解几题，上面题是一号中看到。

kuing

回复 6# 力工

那答案是不是 4？

力工

回复 7# kuing
强，高考题是4，那个题就丢了4。害。

力工

回复 7# kuing
老大，这个怎么搞？

kuing

回复 9# 力工

这不是一样的吗？

kuing

实际上那条二次曲线只提供了调和，所以其实命题可以简化为：

已知梯形的两底分别为 `AD` 和 `BC`，直线 `AB` 与 `CD` 交于 `E`，在直线 `AB` 上取 `F` 使 `A`, `B`, `E`, `F` 为调和点列，记 `S_1=\S{FAD}`, `S_3=\S{FBC}`, `S_2=\S{FCD}`，则 `S_2^2=4S_1S_3`。

注意我这里只是说“两底分别为 `AD` 和 `BC`”并不区分方向，所以有两种情况如下图：

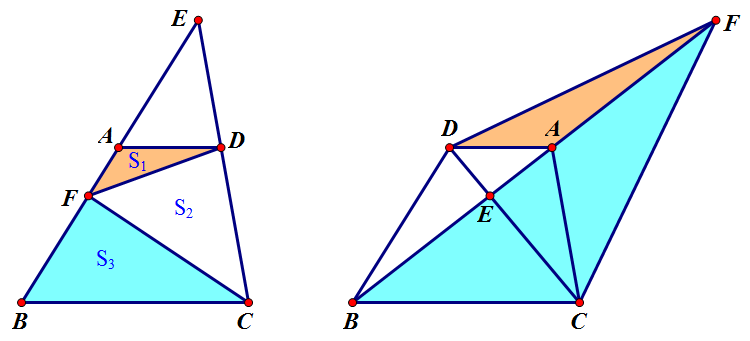
本帖 1# 及 9# 的图是左边的情况，5# 链接里的图则是右边。

两种情况的证明自然也是一样的：
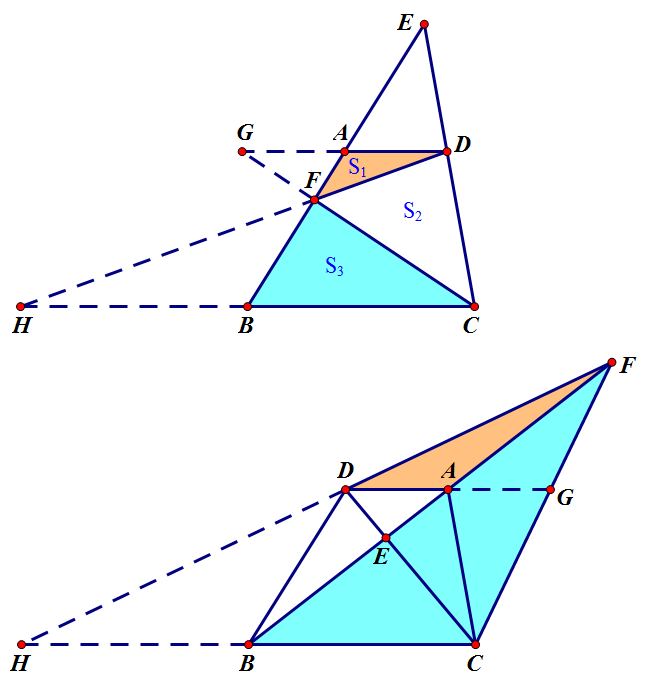
设 `FC` 与 `AD` 交于 `G`，`FD` 与 `BC` 交于 `H`，由平行及调和得
\[\frac{AG}{BC}=\frac{AF}{BF}=\frac{AE}{BE}=\frac{AD}{BC}\riff AG=AD,\]
即 `A` 为 `DG` 中点，同理 `B` 为 `CH` 中点，于是
\begin{align*}
\frac{S_1}{S_2}&=\frac{\frac12\S{FDG}}{\S{FDC}}=\frac{\frac12FG}{FC}=\frac{FA}{2FB},\\
\frac{S_3}{S_2}&=\frac{\frac12\S{FCH}}{\S{FCD}}=\frac{\frac12FH}{FD}=\frac{FB}{2FA},
\end{align*}
相乘即得证。

isee

回复  kuing
老大，这个怎么搞？
力工 发表于 2022-4-29 11:18

知乎的提问题主是你？

kuing

回复 12# isee

这都能找到……

我把 11# 的内容贴过去了，复制粘贴还得改代码，真不方便……画质也比这里差了……

isee

回复 13# kuing

对，知乎不支持$这样的方式，烦极了

kuing

回复 14# isee

不知能否做一个油猴脚本来创建按钮，点一下自动将 $...$ 变成它里面的公式……